Rumfang og overfladeareal bruges til at beregne størrelser på tredimensionelle figurer. I dette indlæg gennemgår vi formlerne for seks forskellige figurer: kasse, cylinder, kugle, kegle, prisme og pyramide.
Helt præcist besvarer vi disse spørgsmål:
Hvad er forskellen på overfladeareal og rumfang?
Hvordan regner man rumfang af en kasse?
Hvordan regner man overfladearealet af en kasse?
Hvordan regner man rumfang af en cylinder?
Hvordan regner man overfladearealet af en cylinder?
Hvordan regner man rumfang af en kugle?
Hvordan regner man overfladearealet af en kugle?
Hvordan regner man rumfang af en kegle?
Hvordan regner man overfladearealet af en kegle?
Hvordan regner man rumfang af et prisme?
Hvordan regner man overfladearealet af et prisme?
Hvordan regner man rumfang af en pyramide?
Hvordan regner man overfladearealet af en pyramide?
Oversigt over formler for rumfang og overfladeareal
Hvad er forskellen på overfladeareal og rumfang?
Når man har en tredimensionel figur, som fx en kasse, en cylinder, en kugle, en kegle eller en pyramide, kan man beregne figurens overfladeareal eller rumfang. Rumfang handler om, hvor meget figuren fylder, og overfladearealet handler om, hvor stor figurens overflade er.
Hvis vi fx har en kasse, svarer kassens rumfang til størrelsen inden i kassen, mens kassens overfladeareal svarer til størrelsen uden på kassen.
Hvordan regner man rumfang af en kasse?
En kasse har seks sider. Alle sider er rektangler, så kassen har en længde, en bredde og en højde, som vist på billedet her:

For at beregne rumfanget af en kasse skal man gange længden, bredden og højden sammen.

I formlen kan du måske se, at l står for længde, b står for bredde, og h står for højde. V står for volumen. Rumfang og volumen er det samme.
Vi kigger på et eksempel. Vi har en kasse med en længde på 5 cm, en bredde på 4 cm og en højde på 3 cm. Regnestykket ser sådan her ud:

Sådan har vi beregnet, at kassen har et rumfang på 60 cm³ (60 kubikcentimeter).
Hvordan regner man overfladearealet af en kasse?
En kasse har som nævnt seks sider. Hvis siderne er rektangler, består de af tre par, hvor hvert par består af to lige store sider. Se billedet her:

De blå sider viser længden ganget med bredden. De gule sider viser længden ganget med højden. De grønne sider viser bredden ganget med højden. Formlen for overfladearealet af en kasse ser derfor sådan her ud:

Som formlen viser, kan man gange længden, bredden og højden parvist sammen og derefter gange de dele med 2, fordi der er to af hver type side.
Lad os beregne samme eksempel fra før, hvor kassens mål er 5 cm x 4 cm x 3 cm. Regnestykket ser sådan ud:

Vi husker at følge regnearternes hierarki, så først skal vi beregne det, der står inde i parentesen, og vi ganger, før vi plusser. Sådan kan vi regne os frem til, at kassen har et overfladeareal på 94 cm² (kvadratcentimeter).
Vær opmærksom på, om du skriver den rigtige enhed, når du skriver dit resultat. Når man finder overfladearealet, finder man en overflade i to dimensioner. Man skriver derfor overfladearealet i kvadratenheder (fx kvadratcentimeter (cm2) eller kvadratmeter (m2)). Når man derimod finder rumfanget, finder man et rum i tre dimensioner. Man skriver derfor rumfanget i kubikenheder (fx kubikcentimeter (cm3) eller kubikmeter (m3)).
Hvordan regner man rumfang af en cylinder?
En cylinder er en figur, der har en cirkelformet top og bund, og så har den en højde, som vist her:

Man finder rumfanget af en cylinder ved at gange cirklens areal med højden. Formlen for arealet af en cirkel ser sådan ud:

(Tegnet π er den matematiske konstant pi, der har en værdi på cirka 3,14.)
Så formlen for rumfanget af en cylinder lyder sådan:

Lad os beregne et eksempel. Vi har en cylinder med en højde på 5 cm og en radius på 3 cm. Regnestykket er derfor:

Vores cylinder har dermed et rumfang på 141,37 cm³.
Hvordan regner man overfladearealet af en cylinder?
En cylinders samlede overflade kan deles op i tre: en top og en bund, der er lige store (det er de lyserøde områder på billedet nedenunder), og den krumme overflade mellem toppen og bunden (det blå område).

Vi finder arealet af den krumme overflade ved at gange cylinderens højde med cirklens diameter. Formlen for en cirkels omkreds kan se sådan her ud:

Vi har set, at man finder arealet af en cirkel ved at gange radius i anden med pi, og vi har to cirkler i cylinderens overflade, så vi ganger med 2. Det lægger vi til den krumme overflade og får dermed denne formel for overfladearealet af en cylinder:


Lad os se på et eksempel, hvor vi igen har en cylinder med en højde på 5 cm og en radius på 3 cm. Regnestykket ser sådan ud:

Vores beregning viser, at cylinderen har et overfladeareal på 150,8 cm².
Hvordan regner man rumfang af en kugle?
En kugle er helt rund og har derfor ikke nogen flade sider. En afstand, som man kan måle i en kugle, er dens radius, dvs. afstanden fra kuglens centrum til periferien (ydersiden).

Man skal derfor kun kende kuglens radius for at beregne kuglens rumfang, og man skal bruge denne formel til beregningen:

Det kan også være, at man kender kuglens diameter. Diameteren er altid dobbelt så lang som radiussen, så hvis man kun kender diameteren, kan man dividere med 2 for at finde radiussen.
Lad os kigge på et eksempel, hvor vi finder rumfanget af en kugle, der har en radius på 4 cm. Regnestykket ser sådan ud:

Sådan har vi beregnet, at kuglen har et rumfang på 268,08 cm³.
Hvordan regner man overfladearealet af en kugle?
Man skal også kun kende kuglens radius (eller diameter) for at finde overfladearealet af kuglen.

Formlen for overfladeareal af en kugle er denne:

Igen kan vi beregne et eksempel, hvor en kugle har en radius på 4 cm. Vi får dette regnestykke:

Altså har kuglen et overfladeareal på 201,06 cm².
Hvordan regner man rumfang af en kegle?
En kegle har en cirkelformet grundflade og en spids top. En kegle fylder en tredjedel af en cylinder, når cylinderen har samme højde og radius.

For at finde rumfanget af en kegle skal vi derfor bruge formlen for rumfang af en cylinder og tage en tredjedel. Formlen for rumfang af en kegle er:

Lad os se på et eksempel, hvor vi har en kegle med en højde på 5 cm og en radius på 3 cm. Vores regnestykke ser sådan ud:

Vi har nu beregnet, at keglen har et rumfang på 47,12 cm³.
Hvordan regner man overfladearealet af en kegle?
Når man skal finde overfladearealet af en kegle, skal man kende keglens radius og sidelængde.

Man finder arealet af den krumme overflade ved at gange pi, radiussen og sidelængden sammen, og vi har set, at man finder arealet af en cirkel ved at opløfte radiussen i anden og gange med pi. For at finde en kegles samlede overfladeareal skal man lægge den krumme overflade og den cirkelformede grundflade sammen.


Lad os beregne et eksempel. Vi forestiller os, at vi har en kegle med en radius på 3 cm og en sidelængde på 7 cm.

Vores kegle har dermed et overfladeareal på 84,25 cm².
Hvordan regner man rumfang af et prisme?
Et prisme er en figur med to ens polygonale grundflader – dvs. en flade med flere lige linjestykker, fx en trekant, en firkant, en femkant osv. En kasse er dermed også et slags prisme, hvor grundfladerne er to rektangler, men i et prisme behøver grundfladerne ikke at være firkantede. Se her, hvor vi har to prismer med henholdsvis en trekantet og en femkantet grundflade:
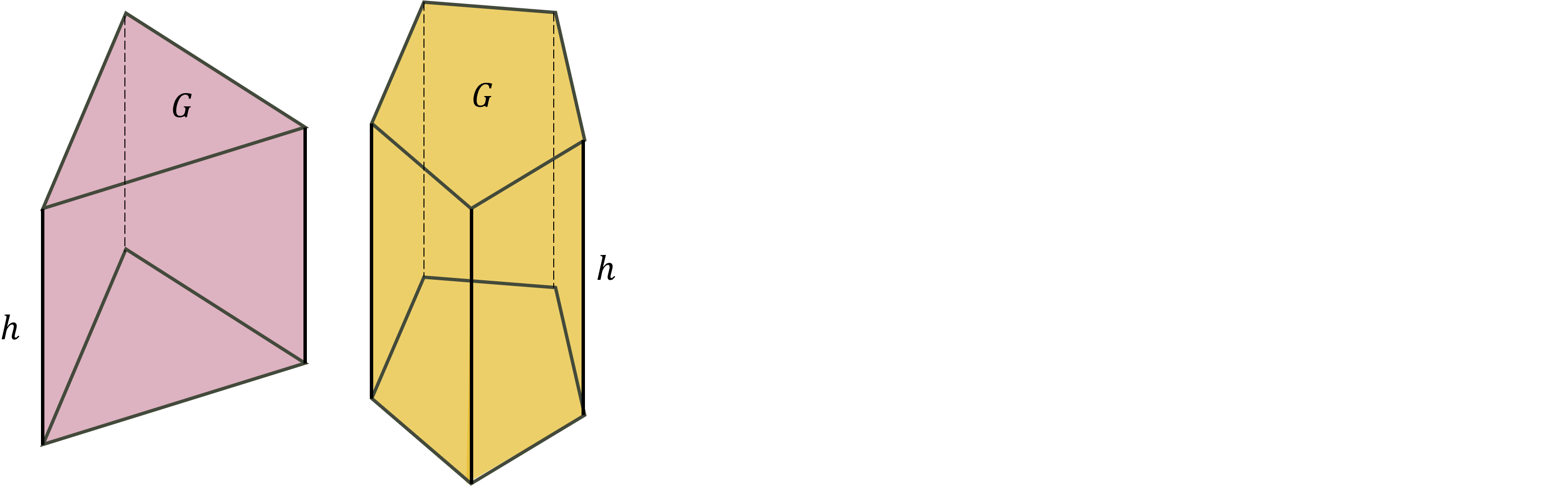
Formlen for rumfanget af et prisme afhænger derfor af, hvilken figur grundfladen er. Generelt lyder formlen for rumfanget af et prisme:

G er altså en generel betegnelse, fordi grundfladen kan have forskellige former og dermed forskellige formler for beregningen af arealet. Lad os tage et eksempel, hvor vi har et prisme med en trekantet grundflade. Formlen for arealet af en trekant er:

Her er g trekantens grundlinje og h trekantens højde. Vi forestiller os, at grundfladen på vores prisme har målene g = 8 cm og h = 5 cm, og at selve prismet har en højde på 12 cm.

Prismet har dermed et rumfang på 240 cm3.
Hvordan regner man overfladeareal af et prisme?
Når man skal finde overfladearealet af et prisme, afhænger det igen af, hvilken figur grundfladen er: en trekant, en firkant, en femkant eller en anden polygonal figur. Generelt lyder formlen for overfladearealet af et prisme:

G er arealet af grundfladen, O er omkredsen af grundfladen, og h er højden på prismet. Vi skal nu også kende omkredsen af grundfladen, som man finder ved at lægge alle sidelængderne (hvad end der er tre, fire, fem eller flere) i polygonet sammen.
Lad os for nemheds skyld tage et eksempel, hvor vores prisme har en retvinklet trekant som grundflade. Vi forestiller os, at trekantens sidelængder er 3 cm, 4 cm og 5 cm:

Vi kan dermed også nemt bestemme trekantens højde og grundlinje, som er h = 3 cm og g = 4 cm.
Derudover forestiller vi os, at selve prismet har en højde på 10 cm, så vi har nu alle vores mål, som vi sætter ind i formlen:
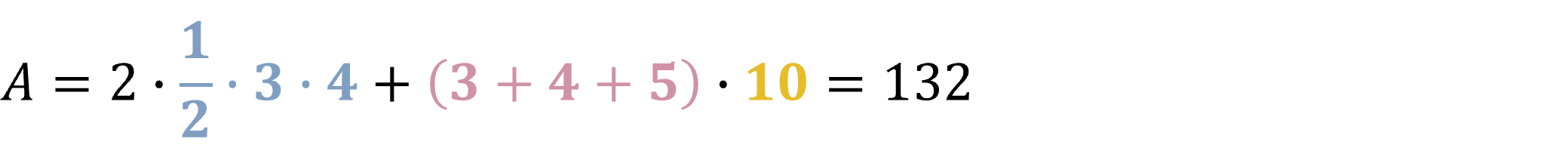
De blå tal er formlen for trekantens areal (G), de lyserøde tal er formlen for trekantens omkreds (O), og det gule tal er prismets højde (h). Sådan har vi beregnet, at vores prisme har et overfladeareal på 132 cm2.
Husk, at G og O afhænger af, hvilken figur prismets grundflader er!
Hvordan regner man rumfang af en pyramide?
En pyramide minder om en kegle, fordi den har en spids top, men i stedet for en cirkelformet flade har en pyramide en polygonal grundflade – dvs. en grundflade med flere lige linjestykker. Ligesom i et prisme kan grundfladen i en pyramide være en trekant, en firkant, en femkant osv. Billedet nedenunder viser en pyramide med en kvadratisk grundflade.

Pyramidens højde er afstanden fra fladen til spidsen, som er vist på figuren med h. Det adskiller sig fra pyramidens sidehøjde (højden på selve siden), som er vist med s på figuren.
Pyramidens grundflade er vist med det lyserøde felt nedenunder. Grundfladens sider har en længde, der er vist med g på figuren. I denne figur er grundfladen kvadratisk, hvilket betyder, at de fire sider er lige lange, og at længden g derfor er den samme, men man kan også have en pyramide, hvor grundfladen har et andet antal sider, eller hvor siderne ikke er lige lange.
Pyramidens ene side er vist med det blå felt nedenunder. Igen har denne figur fire lige store sider, fordi grundfladen er et kvadrat, men det er ikke altid tilfældet.

En pyramide fylder en tredjedel af en kasse, når kassen har samme højde, bredde og længde. Formlen for rumfang af en pyramide er derfor:

Det store G er grundfladens areal. Ligesom vi så ved prismet, er G en generel betegnelse, fordi grundfladen kan have mange former og dermed have forskellige formler for areal. Hvis grundfladen fx er en trekant, skal man sætte formlen for arealet af en trekant ind på G’s plads i ligningen.
Vi kigger på et eksempel med en kvadratisk grundflade. Grundfladens længde er 4 cm, og pyramidens højde er 6 cm. Vi beregner grundfladens areal ved at sige 4 gange 4, så det sætter vi ind på G’s plads:

Sådan har vi beregnet, at pyramidens rumfang er 32 cm³.
Hvordan regner man overfladearealet af en pyramide?
Man finder overfladearealet af en pyramide ved at lægge arealet af grundfladen sammen med arealerne af siderne. Uanset hvad grundfladens form er (fx trekant, firkant, femkant osv.), vil siderne altid være trekantede. Man finder arealet af en trekantet side med denne formel:

Denne formel skal man gange med n antal sider (hvis siderne er lige store) og lægge arealet af grundfladen til, så formlen for overfladearealet af en pyramide er:

Lad os se på et eksempel, hvor vi vil beregne overfladearealet af en pyramide, som har en kvadratisk grundflade. Vi har disse fem arealer, som vi skal lægge sammen:

Dvs. en kvadratisk grundflade og fire lige store sider. Vi forestiller os, at grundfladens længde er 3 cm, og at pyramidens sidehøjde er 7 cm. Regnestykket ser derfor sådan her ud:

Vores pyramide har dermed et overfladeareal på 51 cm².
Vær opmærksom på, at man kun kan gange med n antal sider, når siderne er lige store. Hvis siderne ikke er lige store, skal man beregne arealet af hver side og lægge dem sammen, og så kan man lægge siderne sammen med grundfladen.
Oversigt over formler for rumfang og overfladeareal
Vi har nu gennemgået formler for rumfang og overfladeareal af fem forskellige figurer. Her samler vi dem i en oversigt.
Formel for rumfang af en kasse:

Formel for overfladearealet af en kasse:

Formel for rumfang af en cylinder:

Formel for overfladearealet af en cylinder:

Formel for rumfang af en kugle:

Formel for overfladearealet af en kugle:

Formel for rumfang af en kegle:

Formel for overfladearealet af en kegle:

Formel for rumfang af et prisme:

Formel for overfladearealet af et prisme:

Formel for rumfang af en pyramide:

Formel for overfladearealet af en pyramide:

Der findes andre tredimensionelle figurer, som vi ikke har gennemgået her. Husk, at man kun kan finde rumfang og overfladeareal af tredimensionelle figurer. Man kan ikke finde rumfang og overfladeareal af todimensionelle figurer. Sammenlign figurerne her:

De gule figurer har kun to dimensioner, og de grønne figurer har tre dimensioner. Det betyder, at todimensionelle figurer er flade, mens tredimensionelle figurer har dybde. Man kan derfor ikke beregne overfladeareal eller rumfang af en trekant, et rektangel, en cirkel, et trapez eller nogen andre todimensionelle figurer. Man kan til gengæld finde areal og omkreds af todimensionelle figurer.
Vi håber, at du nu er blevet klogere på rumfang og overfladeareal. Hvis du har svært ved dette eller andet inden for matematik, tilbyder GoTutors dygtige og erfarne undervisere lektiehjælp i matematik.