Statistik går ud på at indsamle nogle data og sætte dem i system. Man præsenterer relevante værdier, som fx gennemsnit, hyppighed, median, nedre og øvre kvartil og meget mere – der er altså mange begreber at holde styr på. Vi gennemgår de centrale begreber i dette indlæg og kommer med eksempler på, hvordan man bruger dem.
Helt præcist kommer vi ind på:
Statistisk: Begreber
Hvad er en hyppighedstabel?
Hvad er en frekvenstabel?
Hvad er typetallet?
Hvad er mindsteværdien og størsteværdien?
Hvordan finder man variationsbredden?
Hvordan finder man gennemsnit?
Hvordan regner man en median ud?
Hvordan finder man nedre og øvre kvartil?
Hvad er et pindediagram?
Hvad kan man aflæse i et boksplot?
Statistisk: Begreber
Inden vi dykker ned i de statistiske beregninger, vil vi gennemgå nogle begreber, som man bruger inden for statistisk. Vi skal nok også forklare begreberne løbende – dette er ment som en oversigt:
Observationer: Tallene i ens data.
Hyppighed: Hvor ofte en observation forekommer i ens data.
Frekvens: Hvor stor en procentdel en observation udgør ud af alle observationerne.
Gennemsnit: Summen af alle observationer divideret med antal observationer.
Typetal: Den oftest forekommende observation.
Mindsteværdi: Den mindste observation i ens data.
Størsteværdi: Den største observation i ens data.
Median: Den midterste observation i ens data.
Nedre kvartil: Den midterste observation i den første halvdel af ens data.
Øvre kvartil: Den midterste observation i den anden halvdel af ens data.
Pindediagram: Et diagram, der viser fordelingen af ens observationer.
Boksplot: Et diagram, hvor man kan aflæse ens mindsteværdi, nedre kvartil, median, øvre kvartil og størsteværdi.
Flere af begreberne kaldes også statistiske deskriptorer (en deskriptor er et tal, som man bruger til at beskrive ens datasæt).
Lad os kigge på et eksempel. En klasse med 25 elever har tilbragt en dag i Tivoli i København. Her har de holdt styr på, hvor mange gange de hver især har prøvet den forlystelse, der hedder Dæmonen. Det kan vi se i skemaet nedenfor:
Hvad er en hyppighedstabel?
Vi har 25 observationer. Vi kan skrive vores observationer i en hyppighedstabel for at få et godt overblik over dem. I en hyppighedstabel kan man se, hvor ofte en observation forekommer – altså hvor hyppig den er.
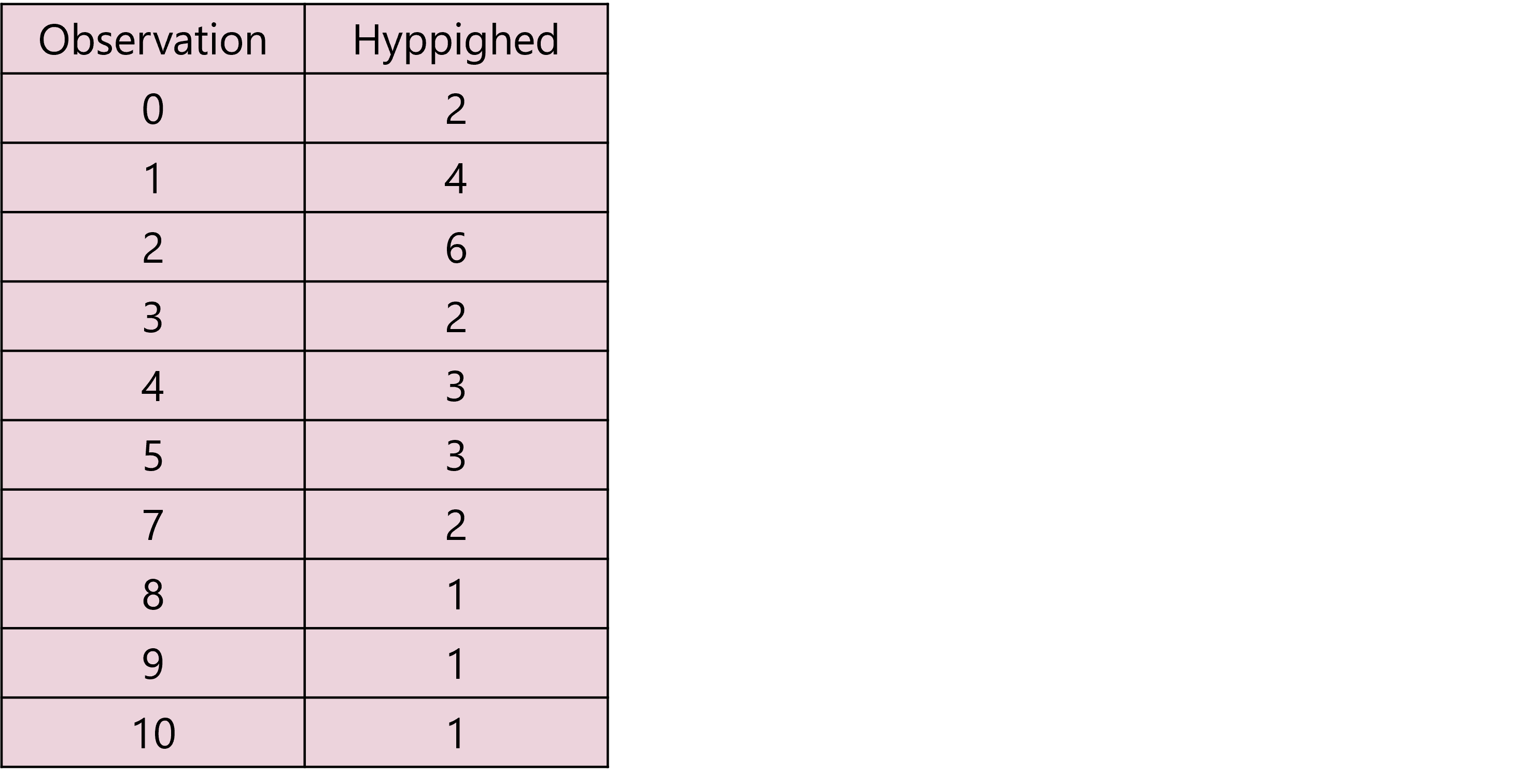
Man læser tabellen ved at se, at 2 af eleverne har prøvet Dæmonen nul gange, 4 af eleverne har prøvet den én gang, 6 af eleverne har prøvet den to gange osv. I venstre kolonne behøver man kun at medtage de observationer, som man har i ens data. Som du kan se, springer vi fx fra 5 til 7 i venstre kolonne, fordi der ikke er nogen af eleverne, der har prøvet Dæmonen seks gange den dag.
Hvad er en frekvenstabel?
Ligesom vi lavede en hyppighedstabel, ønsker vi også at lave en frekvenstabel. Frekvens fortæller, hvor stor en procentdel en observation udgør ud af alle observationerne – altså den relative hyppighed.
For at beregne frekvensen for hver observation, skal vi dividere hyppigheden med det samlede antal observationer, som du kan se i denne tabel:
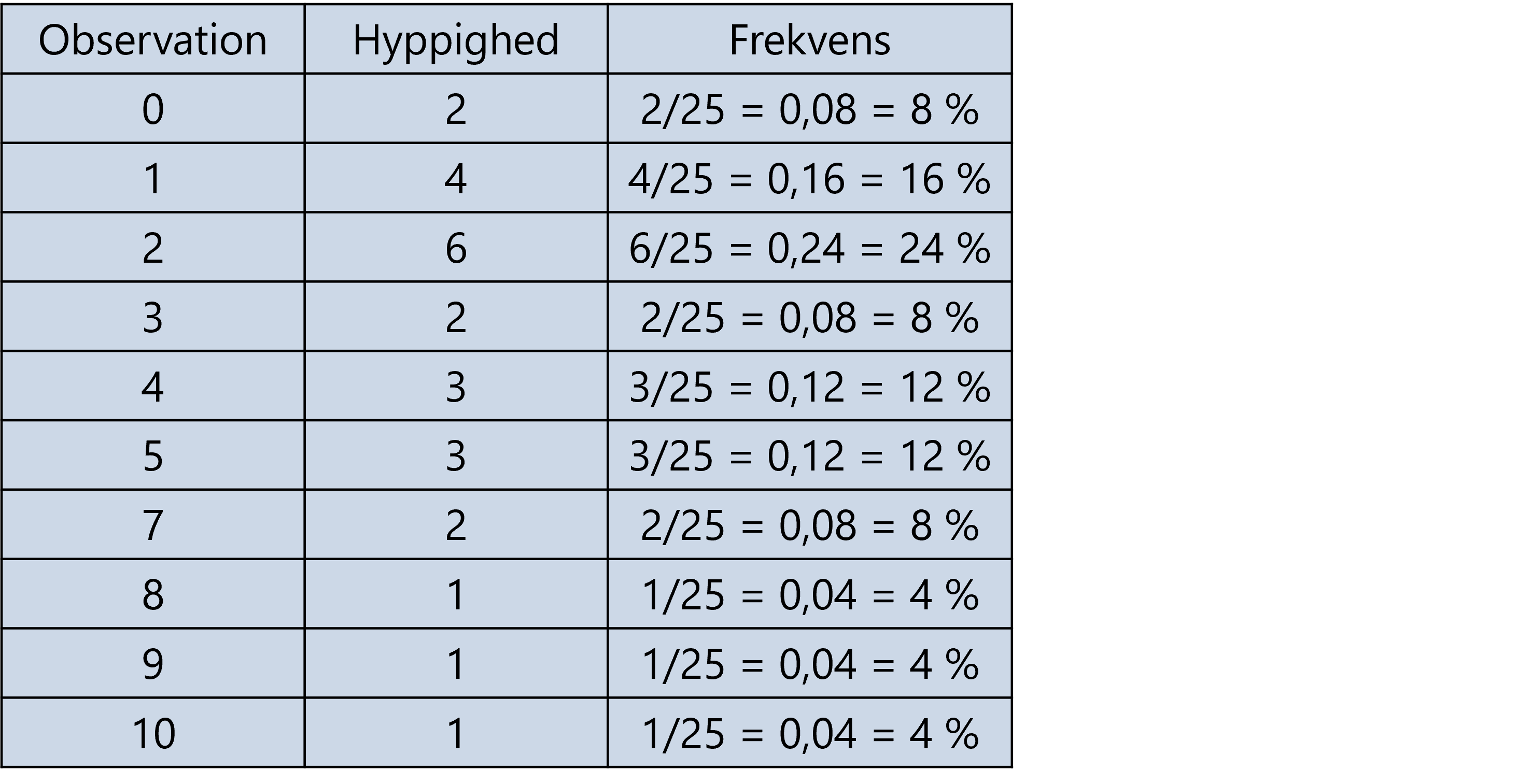
Ud fra tabellen kan vi se, at der fx er 12 % af eleverne i klassen, der har prøvet Dæmonen fem gange.
Som nævnt kan frekvensen også kaldes den relative hyppighed, men hyppighed og frekvens er ikke det samme, som du kan se ovenfor. Hyppighed dækker over et antal, mens frekvens dækker over en andel, som man angiver i procent eller som decimaltal.
Man kan også samle frekvenserne til en summeret frekvens (også kaldet kumulativ frekvens). Den summerede frekvens fortæller, hvor stor en procentdel af observationerne der er mindre end eller lig en given værdi.
Man beregner den summerede frekvens ved at lægge frekvensen til den foregående frekvens. Den samlede summerede frekvens vil altid være 100 %, da dette dækker over det samlede antal observationer.
Således kan vi udvide vores frekvenstabel:
Ud fra tabellen kan vi fx se, at 56 % af eleverne har prøvet Dæmonen tre eller færre gange.
Hvad er typetallet?
Ud fra hyppighedstabellen kan vi også se typetallet. Typetallet er den observation, som vi ser flest gange. I højre kolonne af tabellen kan vi se, at der er flest elever i klassen, der har prøvet Dæmonen to gange, nemlig 6 elever. Derfor er vores typetal 6.
Hvad er mindsteværdien og størsteværdien?
Hyppighedstabellen viser også mindsteværdien og størsteværdien. Mindsteværdien og størsteværdien er den mindste og største værdi i ens data. I vores data er mindsteværdien 0, fordi de elever i klassen, der har prøvet Dæmonen færrest gange, slet ikke prøvede den. I vores data er størsteværdien 10, fordi den elev i klassen, der prøvede den flest gange, prøvede den hele 10 gange.
Hvordan finder man variationsbredden?
Variationsbredden fortæller om spredningen i ens data – altså hvor spredte ens data er. Man finder variationsbredden ved at sige størsteværdien minus mindsteværdien.
10 - 0 = 10
Vores variationsbredde er 10.
Hvordan finder man gennemsnit?
Nu vil vi beregne gennemsnittet (som man også kan kalde ‘middeltallet’ eller ‘middelværdien’). Når vi spørger “Hvor mange gange har eleverne i klassen i gennemsnit prøvet Dæmonen?”, ønsker vi at finde ud af, hvor mange gange hver elev ville have prøvet forlystelsen, hvis de alle havde prøvet den lige mange gange.
Man beregner gennemsnittet ved at tage alle ens observationer og lægge dem sammen, og derefter dividerer man med antal observationer.
Først beregner vi summen af antal ture med forlystelsen for eleverne i hele klassen:
0 + 0 + 1 + 1 + 1 + 1 + 2 + 2 + 2 + 2 + 2 + 2 + 3 + 3 + 4 + 4 + 4 + 5 + 5 + 5 + 7 + 7 + 8 + 9 + 10 = 90
Altså har vi beregnet, at eleverne i klassen tilsammen har prøvet Dæmonen 95 gange. Dette tal dividerer vi med 25 (antal observationer = antal elever i klassen).
90/25 = 3,6
Sådan har vi beregnet, at eleverne i gennemsnit har prøvet Dæmonen 3,6 gange. Det er selvfølgelig ikke muligt for en enkelt person at prøve en forlystelse 3,6 gange, men når man netop beregner et gennemsnit, må ens resultat godt være et decimaltal.
Hvordan regner man en median ud?
Vi ønsker også at finde medianen. Medianen er den midterste observation i ens data, hvis man sorterer sit data i rækkefølge.
Vi skriver derfor vores data i rækkefølge:
For at aflæse det midterste tal kan man krydse et tal af i hver ende, indtil man rammer midten:
Det midterste tal er 3 – derfor er vores median 3.
Det er nemt at finde det midterste tal, når man har et ulige antal observationer. Når man har et lige antal observationer, finder man medianen ved at tage gennemsnittet af de to midterste observationer.
Se fx på denne talrække:
1, 1, 2, 5, 7, 8
De midterste tal er 2 og 5, så vi finder gennemsnittet af dem (og husker at følge regnearternes hierarki) med denne beregning:
(2+5)/2 = 3,5
I ovenstående talrække vil medianen dermed være 3,5.
Vær opmærksom på, at medianen ikke er det samme som gennemsnittet. Mange kommer til at forveksle de to, da ordet ‘middeltallet’ eller ’middelværdien’ (et andet ord for ‘gennemsnittet’) minder om ‘det midterste tal’, men som vist ovenfor er det ikke det samme. Vi har beregnet vores gennemsnit til at være 3,8, og vores median er 3. Det kan dog godt være, at man har et datasæt, hvor ens median og gennemsnit ender med at være det samme tal, men det betyder stadig ikke, at medianen og gennemsnittet viser det samme.
Hvordan finder man nedre og øvre kvartil?
Tilbage til vores eksempel: Vi har lige fundet medianen, og nu ønsker vi også at finde den nedre og øvre kvartil.
Den nedre kvartil kaldes også den 1. kvartil og viser, at 25 % af ens observationer ligger under dette tal.
Medianen kaldes også den 2. kvartil og viser, at 50 % af ens observationer ligger under dette tal.
Den øvre kvartil kaldes også den 3. kvartil og viser, at 75 % af ens observationer ligger under dette tal.
Vi starter med at finde den nedre kvartil. Her skal vi finde det midterste tal af den første halvdel. Da vi fandt medianen ovenfor, delte vi talrækken op i to.
Men skal man så regne medianen med eller ej? Det er der faktisk ikke udbredt enighed om. Lad os sige, at vi ikke regner medianen med. Så har vi denne talrække:
0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2
Den består af 12 tal, altså et lige antal. Man finder den nedre kvartil ved at tage gennemsnittet af de to midterste tal:
(1+2)/2 = 1,5
Men lad os så sige, at vi havde regnet medianen med. Så ville vi have denne talrække:
0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3
Den består af 13 tal, altså et ulige antal, og derfor kan vi nemt finde det midterste tal, som her er 2.
Men er den nedre kvartil så 1,5 eller 2? Vi vælger, at vi ikke regner medianen med, så den nedre kvartil er 1,5 – men spørg hellere din matematiklærer, hvad vedkommende foretrækker!
På samme måde finder vi den øvre kvartil uden at tage medianen med i den anden halvdel af talrækken:
3, 4, 4, 4, 5, 5, 5, 7, 7, 8, 9, 10
Her er vores to midterste tal 5 og 5 – og gennemsnittet af de to er naturligvis bare 5.
Nu startede vi jo med et ulige antal observationer, nemlig 25. Havde vi haft et lige antal observationer, havde det også haft betydning for den nedre og øvre kvartil.
Lad os se på den samme korte talrække fra tidligere:
1, 1, 2, 5, 7, 8
Her fandt vi som bekendt en median på 3,5 ved at tage gennemsnittet af de to midterste tal, men her er der ingen tvivl om, hvordan man deler talrækken i to halvdele, da der er et lige antal.
Første halvdel består af:
1, 1, 2
… og anden halvdel består af:
5, 7, 8
Her er det nemt at finde det midterste tal, men hvis man har to halvdele med et lige antal observationer, ville man igen skulle finde den nedre og øvre kvartil ved at tage gennemsnittet af de to midterste tal i henholdsvis første og anden halvdel af talrækken.
Hvad er et pindediagram?
Vi ønsker nu at præsentere vores fund visuelt. Tallene fra vores hyppighedstabel kan vi sætte ind i et pindediagram (eller et søjlediagram, som i bund og grund er det samme bare med tykkere søjler i stedet for tynde pinde). Vores pindediagram/søjlediagram ser sådan her ud:
Her kan man fx aflæse, at der er fire elever, der har prøvet Dæmonen én gang. Læg mærke til, at vi her – modsat vores hyppighedstabel – har medtaget det antal ture, som ikke passer til nogen af eleverne, nemlig 6 ture.
Hvad kan man aflæse i et boksplot?
Et boksplot er et kasseformet diagram, der viser ens median, nedre og øvre kvartil og mindste- og størsteværdi.
Lad os gentage, hvilke værdier vi fandt ovenover:
Mindsteværdi: 0
Nedre kvartil: 1,5
Median: 3
Øvre kvartil: 5
Størsteværdi: 10
Disse tal kan vi illustrere med et boksplot:
Som du kan se, viser de to ender mindste- og størsteværdien. De to ender af kassen viser den nedre og øvre kvartil, og stregen i midten af kassen viser medianen. Man aflæser værdierne på aksen nedenunder. Fx kan man se, at medianen ligger på 3 på aksen.
Et boksplot deler også ens observationer op i fire dele:
25 % af ens observationer ligger mellem mindsteværdien og den nedre kvartil.
25 % af ens observationer ligger mellem den nedre kvartil og medianen.
25 % af ens observationer ligger mellem medianen og den øvre kvartil.
25 % af ens observationer ligger mellem den øvre kvartil og størsteværdien.
Boksplot er især gode, hvis man sammenligner flere datasæt.
Lad os sige, at de 25 elever også skrev ned, hvor mange gange de hver især prøvede Rutsjebanen, som er en af Tivolis andre forlystelser. Det kan vi se i dette skema:
Igen kan vi skrive alle vores observationer op på en række og finde kvartilsættet:
Vi får disse værdier:
Mindsteværdi: 1
Nedre kvartil: 2
Median: 3
Øvre kvartil: 4
Størsteværdi: 3
Det kan vi også aflæse i et boksplot, som vi sætter ind under det andet for at sammenligne:
Vi kan se, at det nederste boksplot er smallere end det øverste, hvilket betyder, at spredningen er mindre. I eksemplet med Rutsjebanen er variationsbredden 5 (6 - 1 = 5), og i eksemplet med Dæmonen er det 10.
Vi kan også se, at mindsteværdien i eksemplet med Rutsjebanen er større end i eksemplet med Dæmonen. Ved Rutsjebanen er mindsteværdien 1, hvilket betyder, at alle eleverne har prøvet Rutsjebanen mindst én gang, men de har ikke alle prøvet Dæmonen. Til gengæld er størsteværdien noget større ved Dæmonen end ved Rutsjebanen, så den elev, der var vildest med Dæmonen, prøvede den hele 10 gange, mens den elev, der var vildest med Rutsjebanen, prøvede den 6 gange.
Kassen, der viser nedre kvartil, medianen og øvre kvartil, er smallere i eksemplet med Rutsjebanen end i eksemplet med Dæmonen. 50 % af ens observationer ligger i dette interval, og vi kan dermed se, at der er større forskel på, hvor mange ture eleverne har taget med Dæmonen end med Rutsjebanen.
Sådan slutter vores indlæg om statistik. Hvis du stadig søger hjælp – også til andre emner inden for matematik – kan du få lektiehjælp i matematik fra GoTutor.