Procentregning går ud på at regne i hundrededele. Man bruger procentregning i både matematiktimerne og ude i den virkelige verden. Der findes mange regneregler og formler for procentregning, som vi vil vise med eksempler i denne gennemgang. Vi kommer ind på følgende:
Hvad er procent?
Hvordan omregner man procent til decimaltal?
Hvordan omregner man decimaltal til procent?
Hvordan omregner man procent til brøk?
Hvordan omregner man brøk til procent?
Hvor mange procent udgør et tal af et andet?
Hvordan finder man procent af et tal?
Hvordan lægger man procent til et tal?
Hvordan trækker man procent fra et tal?
Hvordan regner man en stigning i procent?
Hvordan regner man et fald i procent?
Hvordan finder man et tal, når man kender en procentdel af det?
Hvordan finder man et tal, når man kender den procentvise stigning?
Hvordan finder man et tal, når man kender det procentvise fald?
Oversigt over regneregler for procentregning
Omvendt procentregning
Procent eller procentpoint?
Hvad er promille?
Beregn moms af et beløb
Beregn avance i procent
Hvad er procent?
Procentregning går ud på at beregne forholdet mellem to tal. Ordet procent betyder ‘hundrededel’. Fx svarer én procent til én hundrededel af et tal. Tal i procent vises med et procenttegn: %.
Vi kan forestille os, at vi skærer en pizza op i fire lige store stykker, og så spiser vi ét stykke. Dette stykke svarer til 25 % af pizzaen, fordi 4 x 25 = 100. Resten af pizzaen svarer til 75 %, og hele pizzaen svarer til 100 %.

Hvordan omregner man procent til decimaltal?
Som nævnt betyder procent ‘hundrededele’. Når man skal omregne fra procent til decimaltal, skal man dividere med 100. Det gør man ved at rykke kommaet to pladser til venstre:
132 % = 1,32
23,5 % = 0,235
1,8 % = 0,018
305 % = 3,05
4 % = 0,04
0,97 % = 0,0097
Hvis man mangler pladser, tilføjer man 0-taller foran. Husk at placere kommaet rigtigt. Et tip er at forestille sig fx 4 som 4,0 – så har man tydeligt et komma, man kan flytte med.
Hvordan omregner man decimaltal til procent?
Når man skal omregne fra decimaltal til procent, skal man omvendt gange med 100. Det betyder, at kommaet skal to pladser til højre:
0,01 = 1 %
0,5 = 50 %
1,923 = 192,3 %
2 = 200 %
45,18 = 4518 %
0,0971 = 9,71 %
Hvis man mangler pladser, kan man altid tilføje 0-taller efter kommaet. Hvis tallet ikke har et komma i forvejen, skal man huske at have det med efter tallet! Altså kan 2 skrives som fx 2,00 – ikke 200.
Hvordan omregner man procent til brøk?
Når man omregner procent til en brøk, skal tælleren være det tal, som man har i procent, og nævneren skal være 100 – igen fordi tal i procent er det samme som antal hundrededele.
Vi tager et eksempel, hvor vi omregner 84 % til en brøk:
Læg mærke til, at det var muligt at forkorte brøken,
Hvis procenttallet indeholder decimaler, skal man først forlænge tæller og nævner, så der ikke længere er nogen decimaler. Hvis vi skal omregne 3,75 % til en brøk, skal vi forlænge brøken med 100, fordi tallet 3,75 indeholder to decimaler. Til sidst forkorter vi brøken mest muligt:

Hvordan omregner man brøk til procent?
Når man skal omregne fra brøk til procent, skal man forlænge eller forkorte brøken, så nævneren er 100.
Vi ser på eksemplet 5/4. Vi skal først have lavet 4-tallet om til 100. Det kan vi nemt gøre ved at dividere 100 med 4, som giver 25. Det betyder, at 4 gange 25 giver 100, så vi skal forlænge brøken med 25 i tæller og nævner.
Når vi har 100 stående i nævneren, viser tælleren tallet i procent.

Lad os også se på eksemplet 7/20. Vi skal først ændre 20 til 100, og det gør vi ved at gange med 5. Derfor skal vi forlænge både tæller og nævner med 5.

Man kan også starte med at omregne brøken til et decimaltal ved at dividere tælleren med nævneren, og derefter kan man gange med 100. Hvis vi igen tager eksemplet 7/20, kan vi dividere 7 med 20, hvilket giver 0,35. Dette ganger vi med 100, som giver 35, så brøken 7/20 svarer til 35 %.
Der kan komme mange situationer, hvor man står med en brøk, som man gerne vil omregne til procent. Det er derfor smart at kende de mest almindelige brøker (fx 1/3, 1/4 eller 2/3) som procent, og på billedet nedenunder kan du se, hvad nogle almindelige brøker svarer til i procent:

Vi har kun taget brøker med, som man ikke kan forkorte yderligere.
Hvis du ikke har helt styr på begreberne 'tæller', 'nævner', 'forkorte' og 'forlænge', kan du læse mere i vores indlæg om brøker.
Hvor mange procent udgør et tal af et andet?
Når man skal beregne, hvor mange procent et tal udgør af et andet tal, skal man dividere de to tal og gange med 100 %. Hvis vi tager udgangspunkt i eksemplet med pizzaen længere oppe på siden, kan vi spørge, hvor meget ét stykke pizza udgør af fire stykker pizza. Her skal vi dividere 1 med 4 og derefter gange med 100 %.
Sådan beregner man, at 1/4 (en fjerdedel) svarer til 25 %.
Man kan med fordel vise divisionsstykket som en brøk. Det er vigtigt at være opmærksom på, at man dividerer tallene rigtigt. Vores udgangspunkt er 4 (hele pizzaen), og vi er interesserede i at finde ud af, hvor meget 1 (et stykke pizza) udgør. Man skal altid dividere med det tal, der er ens udgangspunkt.
Lad os tage endnu et eksempel. Vi har skole med 535 elever. 389 af eleverne plejer at cykle til skole. Nu vil vi gerne beregne, hvor stor en procentdel af eleverne der plejer at cykle til skole. Vi dividerer antal cyklende elever med antal elever i alt, og så ganger vi med 100 %.
Sådan har vi beregnet, at 72,71 % af skolens elever plejer at cykle til skole. Vi kan også afrunde tallet til 72,7 % eller 73 %. Læs mere om afrunding i vores indlæg om decimaltal.
Vi har også lært, at man omregner fra decimaltal til procent ved at rykke kommaet to pladser til højre, så vi kan også bare dividere brøken:
Lad os se på et andet eksempel, hvor vi omregner på de to måder. Vi vil gerne finde ud af, hvor mange procent 125 udgør af 200. Regnestykkerne ser sådan ud:
Begge metoder viser, at 125 udgør 62,5 % af 200.
Hvordan finder man procent af et tal?
Man kan også beregne, hvad en procentdel af et tal svarer til. Vi kan fx forestille os, at vi har fået 5000 kr. i gave, og at vi vil lægge 30 % af pengene over på vores opsparing. Her skal vi dividere 5000 med 100 (for at dele tallet ind i hundrededele), og så skal vi gange med 30 (for at afgøre, hvor mange hundrededele vi har).
30 % af 5000 er 1500, så det betyder, at vi skal lægge 1500 kr. over på vores opsparing.
En anden metode er at omregne procenttallet til et decimaltal og så gange med det. For at finde 30 % af 5000 kan vi nøjes med at gange 5000 med 0,3.
Vi ser på et andet eksempel, hvor vi beregner med begge metoder. Nu vil vi gerne finde ud af, hvor meget 42 % er af 300. Regnestykkerne kan stilles op på disse måder:
Sådan kan vi med to metoder beregne, at 42 % af 300 er 126.
Hvordan lægger man procent til et tal?
Når man lægger procent til et tal, beregner man en del af tallet, som man lægger oveni tallet. Vi kan fx forestille os, at vi lægger 800 kr. ind på vores bankkonto, og så har vi fået 1 % i rente. Det betyder, at banken har givet os 1 % ekstra af vores indestående beløb.
Vi dividerer 1 med 100 for at lave det om til en hundrededel, og det ganger vi med 800 for at finde den hundrededel, som banken vil betale os i rente. Det lægger vi til de 800, som vi har i forvejen.
Sådan har vi vist, at vi ender med et beløb på 808 kr.
En anden metode er at omregne procenttallet til decimaltal og lægge det til 1, og dette decimaltal kan vi gange med det eksisterende tal. I vores eksempel betyder det, at vi omregner en stigning på 1 % til 1,01, og dette ganger vi med de 800.
Igen viser vi de to metoder med et nyt eksempel. Nu vil vi finde ud af, hvordan man lægger 15,5 % til 400. Bemærk, at når procenttallet er et decimaltal, skal vi forlænge brøken, så der ikke er nogen decimaler. Her skal vi forlænge med 10, så 15,5 bliver til 155, og så bliver 100 til 1000.
Sådan kan vi beregne, at 400 plus 15,5 % giver 462.
Vi tager også et eksempel, hvor stigningen er over 100 %. Lad os beregne, hvordan man lægger 134 % til 50.
Vi ganger med 2,34, fordi vi omregner 134 % til 1,34 og lægger det til 1. Vi kan med disse to metoder vise, at 50 plus 134 % giver 117.
Hvordan trækker man procent fra et tal?
At trække procent fra et tal er det modsatte af at lægge procent til et tal, som vi gennemgik lige før. I stedet for at lægge procentdelen til sit eksisterende tal, skal man trække det fra.
Lad os igen forestille os, at vi har 800 kr. stående på vores bankkonto, men nu betaler vi 1 % i negativ rente. Det betyder, at banken tager 1 % af vores indestående beløb.
Formlen er næsten den samme som før, men her er plustegnet byttet ud med minus.
En anden metode er at omregne procenttallet til decimaltal og trække det fra 1, og dette decimaltal kan vi gange med det eksisterende tal. I vores eksempel betyder det, at vi omregner et fald på 1 % til 0,99, og dette ganger vi med de 800.
Vi tager et nyt eksempel med de to metoder. Vi vil nu trække 12 % fra 450.
Vi ganger med 0,88, fordi vi omregner 12 % til 0,12 og trækker det fra 1. Sådan har vi to metoder til at beregne, at 450 minus 12 % giver 396.
Hvordan regner man en stigning i procent?
Man kan beregne en procentvis stigning mellem to tal. Vi kan forestille os, at vi plejer at betale 4000 kr. om måneden i husleje, men nu har vi fået at vide, at vores husleje stiger til 4200 kr. Vi vil gerne finde ud af, hvor meget vores husleje er steget i procent.
Først skal vi finde forskellen mellem de to beløb ved at trække det oprindelige beløb fra det nye. Dette skal vi dividere med det oprindelige beløb for at finde forholdet mellem stigningen og det oprindelige beløb. Til sidst ganger vi med 100 %.
Sådan har vi beregnet, at vores husleje stiger med 5 %.
En anden metode er at dividere de to tal (med det oprindelige tal i nævneren) og trække 1 fra. Så får man et decimaltal, som man kan omregne til procent.
Vi viser de to metoder med et nyt eksempel: Hvor stor er den procentvise stigning, når 40 stiger til 100?
Sådan har vi beregnet, at når 40 stiger til 100, er det steget med 150 %.
Hvordan regner man et fald i procent?
Det modsatte af at beregne en procentvis stigning er at beregne et procentvis fald mellem to tal. Vi kan forestille os, at en vare til 200 kr. er sat ned til 140 kr., og vi er interesserede i at finde ud af, hvor stor en procentvis rabat vi har fået.
Formlen er næsten den samme som før, men her skal vi trække det nye beløb fra det oprindelige beløb.
Vi har beregnet, at prisen er faldet med 30 %.
En anden metode er at dividere de to tal (med det oprindelige tal i nævneren) og trække det fra 1. Så får man et decimaltal, som man kan omregne til procent.
Vi ser på et andet eksempel med begge metoder. Her vil vi beregne det procentvise fald, når 50 falder til 20.
Sådan har vi vist, at når 50 falder til 20, er der sket et fald på 60 %.
Hvordan finder man et tal, når man kender en procentdel af det?
Vi forestiller os, at vi får 15 % rabat på en restaurant, hvor vi ender med at have sparet 45 kr. Nu vil vi gerne finde ud af, hvad det havde kostet, hvis vi ikke havde fået 15 % i rabat.
Først finder vi forholdet mellem rabatten i kroner og rabatten i procent for at finde ud af, hvad én hundrededel af beløbet svarer til. Derefter ganger vi med 100 for at få det fulde beløb.
Sådan har vi beregnet, at beløbet uden rabat ville have været 300 kr.
En anden metode er at omregne procenttallet til et decimaltal og dividere det op i beløbet, som vist her:
I et andet eksempel vil vi gerne finde det oprindelige tal, når vi ved, at 660 svarer til 88 % af det oprindelige tal. Det kan vi som nævnt gøre på disse to måder:
Sådan har vi beregnet, at når 660 svarer til 88 %, svarer det oprindelige tal til 750 (100 %).
Hvordan finder man et tal, når man kender den procentvise stigning?
Vi forestiller os, at vi har fået 2 % udbetalt i rente på vores bankkonto, så vi har 918 kr. stående, og vi vil gerne finde ud af, hvor mange penge vi havde, inden vi fik renten udbetalt.
Tælleren skal indeholde vores nye beløb, og nævneren skal indeholde 100 plus vores procenttal, fordi vores nye beløb udgør 102 % af vores oprindelige beløb. Dette ganger vi med 100 for at få det i procent.
Sådan har vi beregnet, at vi havde 900 kr. på vores bankkonto, inden vi fik 2 % udbetalt i rente.
En anden metode er at omregne procenttallet til et decimaltal og lægge 1 til. Dette dividerer man op i beløbet.
Vi kigger på endnu et eksempel. Et tal er steget med 110 %, så nu er tallet 525, og vi vil gerne finde det oprindelige tal før stigningen. Regnestykkerne ser derfor sådan her ud:
Sådan har vi beregnet, at tallet var 250, inden det steg med 110 % til 525.
Hvordan finder man et tal, når man kender det procentvise fald?
Nu forestiller vi os, at vi skal betale 2 % i rente for at have penge stående på vores bankkonto. Renten er trukket, og vi har 882 kr. stående, så vi vil gerne finde ud af, hvor mange penge vi havde, inden vi betalte renten.
Tælleren skal indeholde vores nye beløb, og nævneren skal indeholde 100 minus vores procenttal, fordi vores nye beløb udgør 98 % af vores oprindelige beløb. Vi ganger dette med 100 for at angive tallet i procent.
Sådan har vi beregnet, at vi havde 900 kr. på vores bankkonto, inden vi betalte 2 % rente.
En anden metode er at omregne procenttallet til et decimaltal og trække det fra 1. Dette dividerer man op i beløbet.
Lad os se på endnu et eksempel. Et tal er faldet med 25 %, så nu er tallet 90, og vi vil gerne finde det oprindelige tal før faldet. Regnestykkerne ser derfor sådan her ud:
Sådan har vi beregnet, at tallet var 120, inden det faldt med 25 % til 90.
Oversigt over regneregler for procentregning
Vi har nu gennemgået ni forskellige regneregler for procentregning, som vi samler i en oversigt her.
Tre regneregler handler om forholdet mellem to tal (fx 400 udgør 80 % af 500). Vi skal kende to ud af tre variabler:
Hele værdien (som fx de 500)
En del af værdien (som fx de 400)
En procentdel (som fx de 80 %)
Vi kender hele værdien og en del af værdien, når vi spørger: Hvor mange procent udgør et tal af et andet? Eksempel:
Vi kender hele værdien og en procentdel, når vi spørger: Hvordan finder man procent af et tal? Eksempel:
Vi kender en del af værdien og en procentdel, når vi spørger: Hvordan finder man et tal, når man kender en procentdel af det? Eksempel:
Tre regneregler handler om en stigning mellem to tal (fx 400 stiger med 25 % til 500). Vi skal kende to ud af tre variabler:
Den originale værdi (som fx de 400)
Den nye værdi (som fx de 500)
Stigningen i procent (som fx de 25 %)
Vi kender den originale værdi og den nye værdi, når vi spørger: Hvordan regner man en stigning i procent? Eksempel:
Vi kender den originale værdi og stigningen i procent, når vi spørger: Hvordan lægger man procent til et tal? Eksempel:
Vi kender den nye værdi og stigningen i procent, når vi spørger: Hvordan finder man et tal, når man kender den procentvise stigning? Eksempel:
Tre regneregler handler om et fald mellem to tal (fx 500 falder med 20 % til 400). Vi skal kende to ud af tre variabler:
Den originale værdi (som fx de 500)
Den nye værdi (som fx de 400)
Faldet i procent (som fx de 20 %)
Vi kender den originale værdi og den nye værdi, når vi spørger: Hvordan regner man et fald i procent? Eksempel:
Vi kender den originale værdi og faldet i procent, når vi spørger: Hvordan trækker man procent fra et tal? Eksempel:
Vi kender den nye værdi og faldet i procent, når vi spørger: Hvordan finder man et tal, når man kender det procentvise fald? Eksempel:
Omvendt procentregning
Hvis man skal beregne en procentdel af et tal i hovedet, er det i mange tilfælde en fordel, hvis man bytter om på rækkefølgen. Som vi har set ovenfor, kan man finde 12 % af 25 ved at gange 25 med 0,12 – men resultatet bliver det samme, hvis man skal finde 25 % af 12, og det er nemmere at beregne, hvad 12 gange 0,25 er, fordi 0,25 svarer til en fjerdedel:
0,25 * 12 = 3
0,12 * 25 = 3
Hvordan kan det være? Når vi lærer at gange, lærer vi, at rækkefølgen er underordnet – fx er det lige meget, om man siger 4 * 7 eller 7 * 4.
Generelt kan vi finde X % af Y på denne måde:
X * 0,01 * Y
… fordi procent betyder hundrededel, så X % svarer til at skrive X * 0,01. Som nævnt er rækkefølgen underordnet, når man ganger, så vi kunne også skrive:
Y * 0,01 * X
Det er så det samme, som hvis man skrev Y % af X, og derfor får man samme resultat, som hvis man sagde X % af Y.
Procent eller procentpoint?
Ovenstående regneregler handler om to tal og en procentdel, men man kan også have at gøre med to procentdele. Vi kan fx forestille os, at et politisk parti har fået 15 % af stemmerne til et valg, hvilket er en stigning fra forrige valg, hvor de fik 10 % af stemmerne. Denne stigning kan man beregne på to måder:
Vi kan beregne den absolutte forskel ved at trække 10 fra 15. Det er en stigning på 5 procentpoint.
Vi kan også beregne den relative forskel ved at dividere 15 med 10 og trække 1 fra. Det giver 0,5 og er dermed en stigning på 50 %.
Ligeledes kan man beregne et fald mellem to procentsatser. Vi forestiller os, at et andet politisk parti er gået fra 26 % af stemmerne til 20 %.
Den absolutte forskel: 26 - 20 = 6 procentpoint
Den relative forskel: 26/20 - 1 = 0,3 = 30 %
Det kan godt være en anelse svært at forstå, at 10 % stiger med 50 % til 15 %, og at 26 % falder med 30 % til 20 %. Derfor kan procentpoint være en nemmere måde at forstå ændringer mellem to procentsatser.
Lad os vise nogle flere eksempler:
En stigning fra 30 % til 75 %:
Den absolutte forskel: 75 - 30 = 45 procentpoint
Den relative forskel: 75/30 - 1 = 1,5 = 150 %
Et fald fra 200 % til 40 %:
Den absolutte forskel: 200 - 40 = 160 procentpoint
Den relative forskel: 200/40 - 1 = 4 = 400 %
Det er vigtigt, at man ikke blander procent og procentpoint sammen. Som du nu har set, betyder det noget meget forskelligt.
Hvad er promille?
Ligesom procent betyder ‘hundrededel’, betyder promille ‘tusindedel’. Ordenes oprindelse stammer fra latin, hvor pro- betyder ‘for hver’, centrum betyder ‘hundrede’, og mille betyder ‘tusinde’, så procent betyder ‘for hver hundrede’, og promille betyder ‘for hver tusinde’.
Tal i promille vises med et promilletegn: ‰.
Bemærk, at ordet promille også bruges til at beskrive, hvor meget alkohol en person har i blodet (fordi denne koncentration måles i tusindedele), men i denne matematik-sammenhæng bruger vi det blot om tusindedele.
Man beregner promille på samme måde som procent – bare ved at dividere med 1000 i stedet for med 100. Eksempler:
En promille af 1000: 1000/1000 = 1 ‰
En promille af 100: 100/1000 = 0,1 ‰
En promille af 10: 10/1000 = 0,01 ‰
En promille af 1: 1/1000 = 0,001 ‰
Beregn moms af et beløb
Selvom vi allerede har gennemgået de forskellige regneregler for forholdet mellem to tal, er der en bestemt størrelse, der her får sit eget afsnit: moms.
Moms er en afgift på en vare, som (for hvert trin den bliver solgt mellem producent, forhandlere og forbruger) skal betales til staten. Denne afgift er en fast procentsats af varens værdi.
Forskellige lande har forskellige momssatser. I Danmark er momsen 25 %.
Når man beregner moms, skal man være opmærksom på, om man lægger momsen til, eller om man trækker momsen fra. Der er nemlig forskel, og det viser vi her med nogle eksempler.
Vi har en vare til 800 kr., og vi skal lægge 25 % moms til. Det kan vi gøre på disse to måder:


Når et beløb uden moms er 800 kroner, er beløbet med moms 1.000 kroner.
Men lad os så vise, hvorfor man skal være opmærksom, hvis man skal regne omvendt og trække momsen fra. Så skal man nemlig ikke trække 25 % fra som her:


Beløbet uden moms skal nemlig give 800 kroner. Når man trækker momsen fra et beløb, skal man derfor trække 20 % fra. Se her, hvordan udregningerne nu passer:


Husk derfor på:
Når man skal lægge moms til, er det 25 %.
Når man skal trække moms fra, er det 20 %.
Måske kan dette billede hjælpe dig med at forstå, hvorfor det hænger sådan sammen:
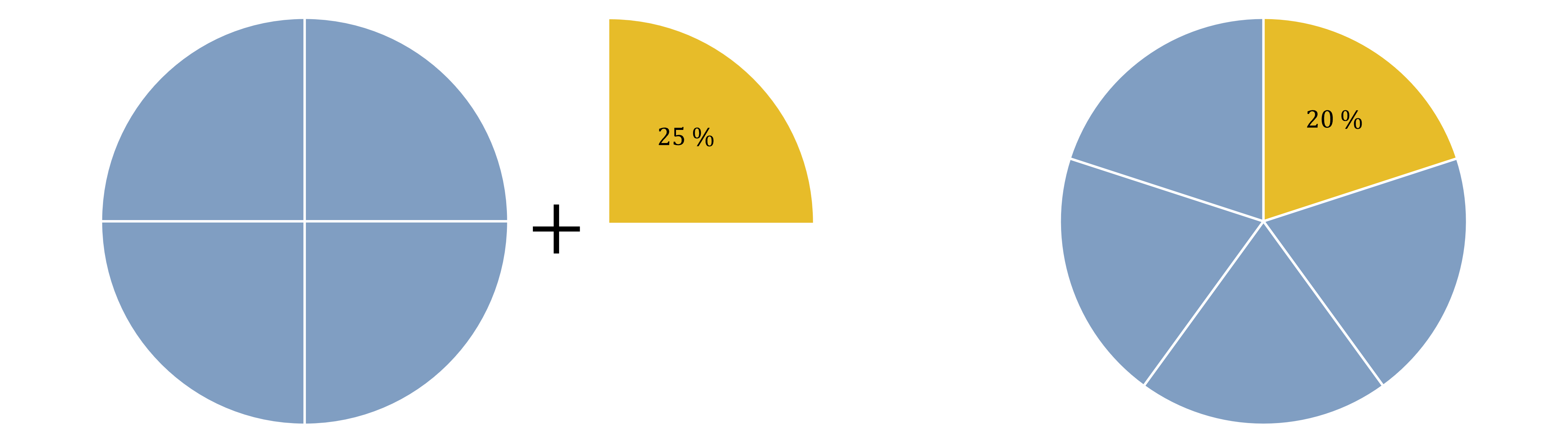
Til venstre har vi et beløb uden moms (den blå cirkel). Vi lægger momsen oven i (det gule cirkeludsnit), som er 25 %. Momsen udgør nu en femtedel af hele beløbet.
Til højre har vi et beløb med moms (hele cirklen). Momsen udgør stadig en femtedel af hele beløbet, så når vi trækker denne femtedel fra (det gule cirkeludsnit), udgør det 20 %.
Beregn avance i procent
Også her bruger vi nogle regneregler, som vi allerede har gennemgået, men som du her kan se, hvordan man helt specifikt bruger dem om: avancen.
Avancen er forholdet mellem salgsprisen og indkøbsprisen af en vare – fx hvad en butik sælger en vare for til kunden (salgsprisen), og hvad butikken selv har betalt i omkostninger for levering og salg af varen til butikken (indkøbsprisen).
Man kan beregne avancen i kroner og i procent.
Eksempel: Vi ønsker at beregne avancen i kroner, når vi har en salgspris på 250 kroner og en indkøbspris på 160 kroner.
250 - 160 = 90 kr.
Avancen (fortjenesten) på varen er derfor 90 kroner. Det er et simpelt minusstykke, som vi naturligvis også kan beregne i procent.
Eksempel: Vi ønsker at beregne avancen i procent, når vi har en salgspris på 250 kroner og en indkøbspris på 160 kroner.

Når en vare købes ind for 160 kroner og sælges til 250 kroner, er avancen (fortjenesten) dermed 36 %.
Det kan også være, at man kender salgsprisen og avancen i kroner og gerne vil beregne avancen i procent.

Sådan beregner man avancen i procent.
Vi har nu gennemgået en masse forskellige regler for procentregning. Vi har også vist, hvordan man omregner mellem procent, brøk og decimaltal, og vi har forklaret forskellen på procent og procentpoint. Hvis du stadig sidder og bøvler med at forstå procentregning, kan du finde lektiehjælp i matematik hos GoTutor.