Når du lærer om differentialligninger i matematiktimen, har du sikkert allerede lært om ligninger og differentialregning. Derfor kan vi kort opsummere, at man løser en ligning med en ubekendt ved at finde værdien af den ubekendte, og at man laver differentialregning ved at finde en funktions afledede funktion.
I dette indlæg får du en kort gennemgang af, hvad differentialligninger er, og hvordan man løser dem.
Det kan godt virke svært og kompliceret. Har du brug for ekstra hjælp, står GoTutor klar med dygtige og erfarne lektiehjælpere, der kan tilbyde lektiehjælp i matematik på alle niveauer i gymnasiet.
Hvad definerer en differentialligning?
En differentialligning indeholder en afledet funktion, og man løser differentialligningen ved at finde funktionen til den afledede funktion. Det adskiller sig fra ligninger, som man løser ved at finde frem til et tal – ved differentialligninger er løsningen en funktion.
Forskriften for en funktion er ofte f(x), så forskriften til den afledede funktion bliver f’(x) (altså “f mærke af x”). Det gælder, at f(x) = y, så i differentialligninger ser man som regel den afledede funktion skrevet som y’ (eller dy/dx).
Et eksempel på en differentialligning kunne derfor være:
(Bemærk, at det er den samme differentialligning skrevet på to forskellige måder.)
For at finde funktionen til den afledede funktion skal vi integrere på begge sider af lighedstegnet:
y’ = 4x
y = 2x²
Hvis vi har funktionen f(x) = 2x², ville den afledede funktion være f’(x) = 4x. Men hvad hvis vi havde funktionen f(x) = 2x² + 7 og ville finde den afledede funktion?
y = 2x² + 7
y’ = 4x
Det ville også blive y’ = 4x. Når man integrerer en funktion, kan man ikke bestemme værdien af konstanten, og differentialligningen har derfor uendeligt mange løsninger.
Man kan derfor skrive løsningen på denne måde:
y = 2x² + k
… hvor k er en konstant.
Hvis konstanten er lig med 0, ser grafen for vores løsning sådan her ud:
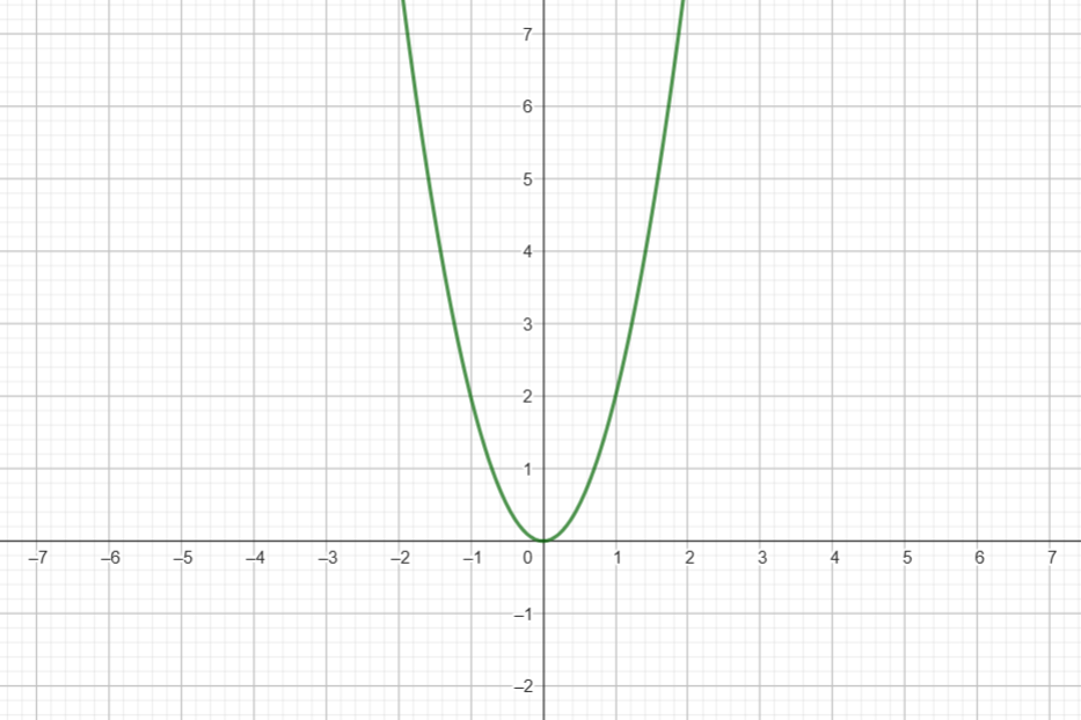
Dette kalder man en løsningskurve eller en integralkurve. Men som bekendt har differentialligningen uendeligt mange løsninger, så løsningskurven kunne for eksempel også ligge disse steder:
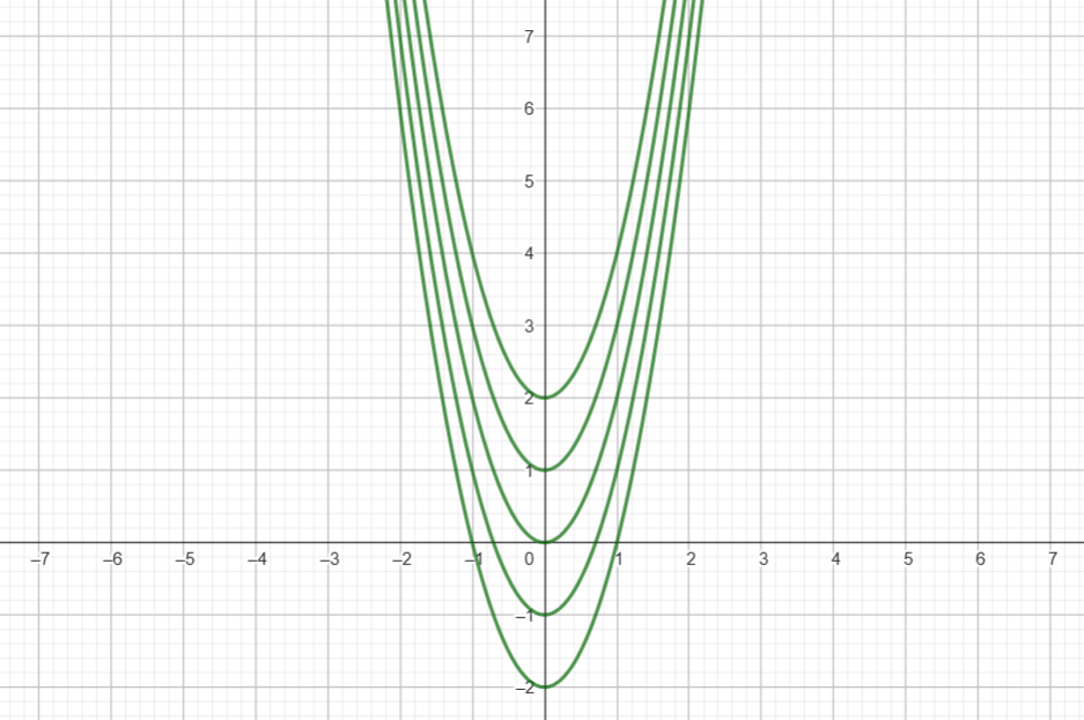
Når man ikke kan bestemme værdien af konstanten, siger man, at dette er den fuldstændige løsning til differentialligningen (altså samtlige løsninger). Men man kan også blive bedt om at finde en partikulær løsning (en specifik løsning). Her vil man typisk få en startbetingelse, der bestemmer, hvilken partikulær løsning der er gældende.
En differentialligning med en startbetingelse kunne se sådan her ud:
y’ = 4x, y(2) = 19
Det betyder, at grafen for løsningskurven går gennem punktet (2, 19). Det første trin er at finde den fuldstændige løsning:
y = 2x² + k
Næste trin er at indsætte vores givne punkt (2, 19) i ligningen, så vi kan isolere k:
19 = (2*2)² + k
19 = 16 + k
19 - 16 = k
k = 3
Den partikulære løsning vil derfor være:
y = 2x² + 3
Det er dog ikke altid, at du i din matematikopgave bliver spurgt, hvad løsningen til differentialligningen er. I stedet kan du få en differentialligning og en løsning i form af en funktion og blive spurgt, om løsningen passer til differentialligningen.
Her skal du sætte funktionen ind på begge sider af lighedstegnet. Hvis det giver det samme, er løsningen korrekt, og hvis ikke, er den naturligvis forkert.
Vi har fx denne differentialligning:
4y - y’ = 4x² + 10x + 3
Vi bliver spurgt, om denne funktion er løsningen til differentialligningen:
f(x) = x² + 3x
Vi starter med at differentiere funktionen f:
f’(x) = 2x + 3
Nu kan vi sætte værdierne for y og y’ ind i differentialligningen:
4*(x² + 3x) - 2x + 3 = 4x² + 10x + 3
4x² + 12x - 2x + 3 = 4x² + 10x + 3
4x² + 10x + 3 = 4x² + 10x + 3
Der står det samme på begge sider af lighedstegnet, så det er sandt, at funktionen f er løsningen til differentialligningen.
Lad os kigge på et andet eksempel. Vi bliver spurgt, om denne funktion:
f(x) = 2x + 3x²
… er løsningen til denne differentialligning:
y’ - 3y = 2 - 9x²
Før valgte vi at differentiere funktionen, inden vi satte den ind i ligningen, men man kan også vælge at gøre det i mellemregningerne:
(2x + 3x²)’ - 3*(2x + 3x²) = 2 - 9x²
2 + 6x - 6x - 9x² = 2 - 9x²
2 - 9x² = 2 - 9x²
Læg mærke til, at vi differentierede f, så den afledede funktion blev f’(x) = 2 + 6x. Vi fik det samme på begge sider af lighedstegnet, så løsningen med funktionen f er sand.