Fibonacci-tal støder vi på i bl.a. matematikken, i naturen og i billedkunsten. Men hvad er Fibonacci-tal, og hvorfor ser de ud, som de gør?
Det gennemgår vi i dette indlæg, hvor vi kommer ind på følgende:
Hvad er Fibonacci-tal?
Sammenhænge i Fibonacci-talrækken
Baggrunden for Fibonacci-tal
Fibonacci-tallene og det gyldne snit
Fibonacci-tal med Binets formel
Fibonacci-tal i naturen
Hvad er Fibonacci-tal?
Fibonacci-tal er en talrække, der starter med 0, så 1, og så summen af de to foregående tal. På den måde fortsætter rækkefølgen i det uendelige. De første 30 Fibonacci-tal er:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10.946, 17.711, 28.657, 46.368, 75.025, 121.393, 196.418, 317.811, 514.229
Vi kan illustrere, hvorfor rækkefølgen ser ud, som den gør:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
55 + 89 = 144
89 + 144 = 233
… og sådan fortsætter det.
Vi kan også vise det med dette billede:
Talrækken følger dermed denne formel:
Fn+1 = Fn + Fn-1
Bemærk, at n ikke er selve tallet, men nummeret i rækkefølgen (her regnes 0 dog ikke med i rækkefølgen). Hvis vi tager udgangspunkt i det syvende tal (n = 7) i rækkefølgen, som er 13, skal man lægge det sammen med det sjette tal (n = 7-1) i rækkefølgen, som er 8, for at finde det ottende tal (n = 7+1) i rækkefølgen:
13 (F7) + 8 (F7-1) = 21 (F7+1)
Hvis vi tager kvadraterne af hvert Fibonacci-tal, danner de nedenstående mønster, hvor et kvadrat er præcist lige langt som de to foregående (fordi et Fibonacci-tal som nævnt er summen af de to foregående).
Sammenhænge i Fibonacci-talrækken
Der er flere sammenhænge i Fibonacci-talrækken, der gør talrækken lidt spøjs.
For eksempel er der en sammenhæng mellem talrækken, som de står, og hvis de er opløftet i anden potens:
F | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | … |
F² | 1 | 1 | 4 | 9 | 25 | 64 | 169 | 441 | … |
Sammenhængen er, at hvis du vælger et tal i Fibonacci-talrækken, er summen af alle F²-tallene op til dette tal det samme, som hvis du ganger dit Fibonacci-tal med det næste tal i talrækken.
Hvis vi vælger Fibonacci-tallet 2, får vi det samme resultat på to måder:
1 + 1 + 4 = 6
2 × 3 = 6
Hvis vi vælger Fibonacci-tallet 8, får vi det samme resultat på to måder:
1 + 1 + 4 + 9 + 25 + 64 = 104
8 × 13 = 104
Dette gælder alle steder i talrækken.
En anden sammenhæng ser man, når man udvælger fem tal i rækkefølge hvor som helst i talrækken. Hvis man tager det første og det sidste af disse fem tal og lægger sammen og derefter dividerer med 3, får man det midterste af de fem tal.
Eksempel: Vi ser på rækkefølgen 2-3-5-8-13:
2 + 13 = 15
15 : 3 = 5 (det midterste tal er 5)
Vi ser også på rækkefølgen 13-21-34-55-89:
13 + 89 = 102
102 : 3 = 34 (det midterste tal er 34)
Dette gælder også alle steder i talrækken.
Prøv selv at se, om du kan finde flere sammenhænge!
Baggrunden for Fibonacci-tal
Fibonacci-talrækken har fået sit navn efter den italienske matematiker Leonardo Fibonacci, som opdagede talrækken ved at spørge, hvordan bestanden af kaniner ville vokse, hvis man startede med ét par kaniner, som parrede sig, når de var én måned gamle og fik ét par kaniner efter yderligere en måned og herefter hver måned (så kaninerne fik to unger, når de var både to måneder gamle, tre måneder gamle, fire måneder gamle osv.) – og det samme ville ungerne (de nye par af kaniner) gøre. Lad os forklare:
Efter den første måned ville der være 1 par kaniner, som er én måned gamle, og som derfor har parret sig.
Efter den anden måned ville der være 2 par: det første kaninpar, som nu er to måneder gamle, plus det kaninpar, der lige er født.
Efter den tredje måned ville der være 3 par: det første kaninpar, som nu er tre måneder gamle, og som derfor har fået to kuld: det par, som nu er en måned gamle og kan parre sig, plus et nyfødt par.
Efter den fjerde måned ville der være 5 par: det første kaninpar, som nu er fire måneder gamle, og som derfor har fået tre kuld: det par, som nu er to måneder gamle, som har fået deres første kuld; det par, som nu er én måned gamle og kan parre sig; og det nyfødte par.
Man kan også forstå det sådan her:
Kaninpar A parrer sig (1 par i alt).
Kaninpar A bliver forældre til kaninpar B (2 par i alt).
Kaninpar A bliver forældre til kaninpar C, og kaninpar B parrer sig (3 par i alt).
Kaninpar A bliver forældre til kaninpar D, kaninpar B bliver forældre til kaninpar E, og kaninpar C parrer sig (5 par i alt).
Kaninpar A bliver forældre til kaninpar F, kaninpar B bliver forældre til kaninpar G, kaninpar C bliver forældre til kaninpar H, kaninpar D parrer sig, og kaninpar E parrer sig (8 par i alt).
Det er naturligvis kun teoretisk, og derfor skal det tænkes, at alle kaninpar får præcis to unger hver måned efter den anden måned, og at ingen kaniner dør undervejs. På den måde kan bestanden af kaniner vokse i dette bestemte mønster.
Fibonacci-tallene og det gyldne snit
Fibonacci-tal findes også inden for billedkunsten, fordi talrækken har dannet grund for det gyldne snit. Det gyldne snit er en måde, hvorpå man inddeler sit billede i nogle felter og placerer de vigtigste elementer i ens motiv i forhold til de felter, så øjet fanger disse elementer først. Mange kunstnere og fotografer bruger dermed det gyldne snit i deres billeder.
Det er dog ikke sikkert, at de præcist kender matematikken bag. Når man tegner det gyldne snit, går det ud på at dele et linjestykke i en længere del (a) og en kortere del (b). Forholdet mellem a og b skal være det samme som forholdet mellem hele linjestykket og a, som vist med denne beregning:
Som du kan se, får vi en konstant på cirka 1,618. Det betyder, at a skal være 1,618 gange længere end b, og at a og b lagt sammen skal være 1,618 gange længere end a. Man kan også beregne konstanten (som hedder phi og skrives med det græske bogstav φ) på denne måde:
Hvordan hænger det sammen med Fibonacci-talene? Ser du, når man dividerer et Fibonacci-tal med det foregående tal, kommer man tæt på værdien af phi – faktisk kommer man tættere og tættere på, jo større tallene er.
Det er altså endnu en sammenhæng mellem tallene.
Fibonacci-tal med Binets formel
Konstanten φ, som vi beregnede ovenfor, kan også bruges til at finde et Fibonacci-tal med Binets formel, som lyder:

Hvis vi skriver værdien for φ ind i formlen, ser den sådan her ud:
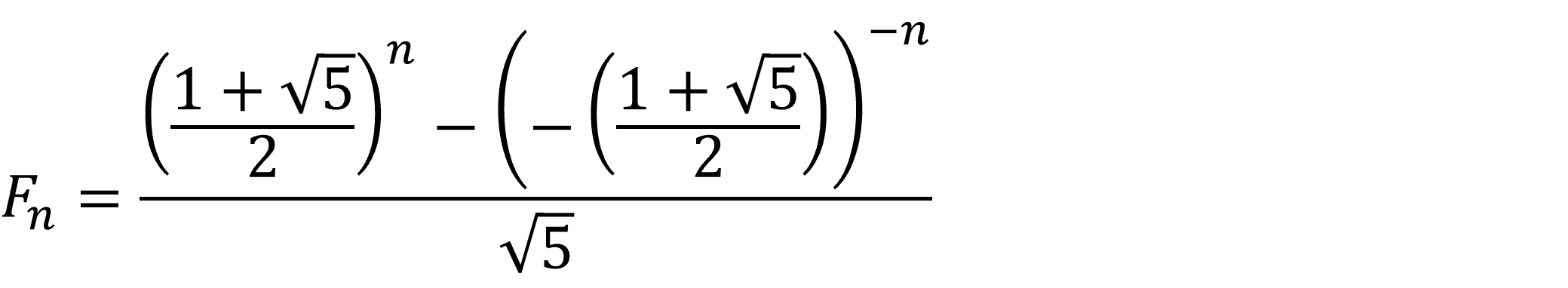
Også her er n nummeret i rækkefølgen – ikke selve Fibonacci-tallet. Vi kan fx finde det 10. Fibonacci-tal ved at sætte 10 ind på n’s plads i formlen:
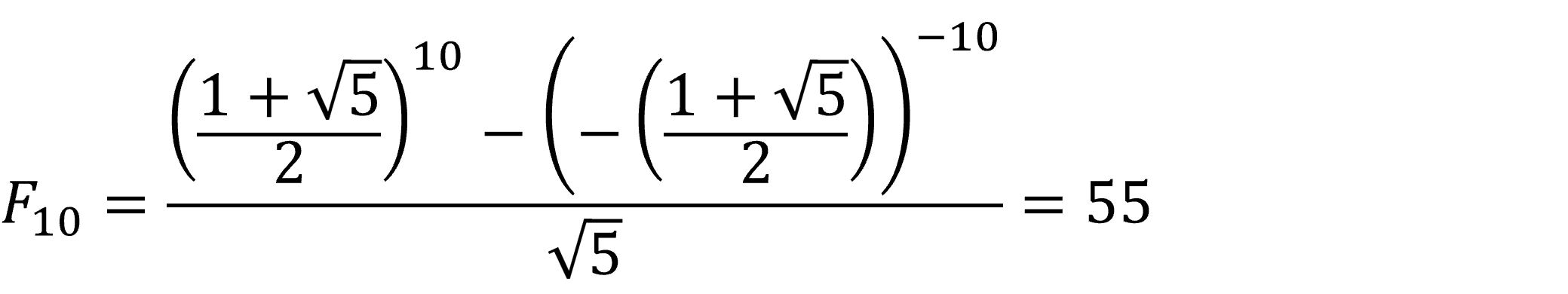
Sådan har vi fundet frem til, at det 10. Fibonacci-tal i rækken (hvis vi ser bort fra 0) er 55. Det er naturligvis en kringlet beregning, så vi anbefaler at bruge et regneprogram.
Man kan dermed bruge Binets formel til at finde et Fibonacci-tal uden at skulle kende de to foregående tal i rækkefølgen. Binets formel er opkaldt efter den franske matematiker Jacques Philippe Marie Binet.
Fibonacci-tal i naturen
Man støder også på Fibonacci-tal ude i naturen. Flere planter og træer vokser i et spiralmønster, der passer med kvadraterne til Fibonacci-tallene, nemlig dette:
Fibonacci-tallene viser sig fx i måden, hvorpå blade på en stilk placerer sig i forhold til hinanden, og hvorpå træer forgrener sig. Man ser det også i måden, hvorpå blomsterbladene på en artiskok, kernerne på en solsikke, skællene på en grankogle og spirene på en ananas arrangerer sig. Fx ser man ofte, at frugtspirene på en ananasplante deler sig i to retninger, så den får otte spirer i den ene ende og 13 spirer i den anden ende – altså passer det med to Fibonacci-tal.