I dette indlæg kan du blive klog på, hvad omvendt proportionalitet er – og først og fremmest hvad proportionalitet helt generelt betyder. Vi kommer nemlig ind på:
Hvad betyder ligefrem proportionalitet?
Hvad er omvendt proportionalitet?
Ligefrem og omvendt proportionalitet: eksempel
Hvad kaldes graferne for omvendt proportionale funktioner?
Hvis du søger hjælp til flere emner inden for matematik, kan du tjekke GoTutors matematikblog, som bygger på vores mange års erfaring med lektiehjælp i matematik.
Hvad betyder ligefrem proportionalitet?
En størrelse er proportional med en anden størrelse, når den varierer i samme forhold til den anden størrelse – det vil sige, at de to størrelser “følges ad” ved at vokse eller aftage, når den anden også vokser eller aftager. Begrebet proportionalitet er afledt fra det latinske proportio, som betyder ‘ligeligt forhold’.
Lineære funktioner er et eksempel, der viser ligefrem proportionalitet eller direkte proportionalitet. Når x-værdien vokser eller aftager med en fast værdi, vokser/aftager y-værdien også med en fast værdi. Det skriver vi med denne forskrift:
Vi kommer med et konkret eksempel længere nede, men først vil vi forklare, hvordan det adskiller sig fra omvendt proportionalitet.
Hvad er omvendt proportionalitet?
Ved omvendt proportionalitet gælder det, at når den ene størrelse vokser, så aftager den anden størrelse – og når den ene størrelse aftager, så vokser den anden størrelse. Det skriver vi med denne forskrift:
x kan ikke være 0, da man ikke kan dividere med 0. Det skriver vi på denne måde:
x ≠ 0
Ved ligefrem proportionalitet gælder det, at hvis x fx fordobles, så fordobles y også, og hvis x halveres, så halveres y også. Men ved omvendt proportionalitet er det – som navnet antyder – omvendt: hvis x fordobles, så halveres y, og hvis x halveres, så fordobles y.
Ligefrem og omvendt proportionalitet: eksempel
Lad os vise et eksempel på både ligefrem og omvendt proportionalitet. Hvis vi står i en butik og skal købe æbler, skal vi betale mere, jo flere æbler vi køber. Forholdet mellem antallet af æbler og den samlede pris er ligefrem proportionalt.
Hvis et æble koster 2,50 kroner stykket, kan du se på billedet her, hvordan vi skal betale mere, jo flere æbler vi køber:
Vi skriver eksemplet op på denne måde:
Her er x antal æbler, og y er den samlede pris.
Forestil dig nu, at vi skal spise en lagkage. Jo flere personer vi er om at deles om kagen, des mindre stykker kan vi hver især få. Forholdet mellem antallet af personer og størrelsen på kagestykkerne er derfor omvendt proportionalt.
På billedet her kan du se, hvordan et stykke bliver mindre, hvis flere personer skal dele kagen:
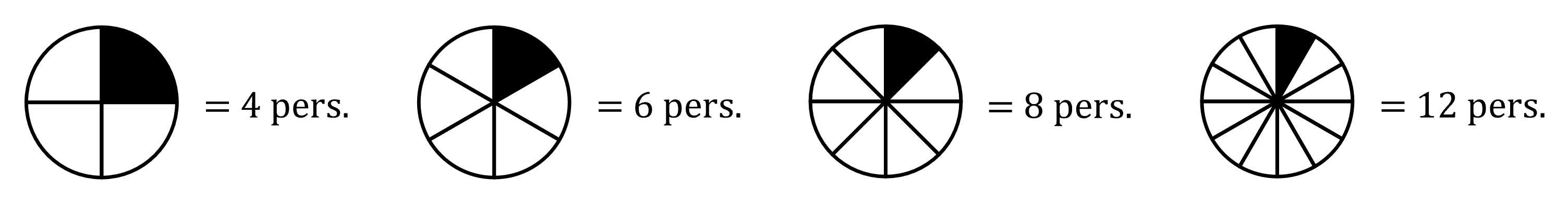
Vi skriver eksemplet op på denne måde:
Her er x antal personer, og y viser, hvor stor en brøkdel af kagen, man får. a er 1, fordi der er én kage, og som altid gælder det, at x ≠ 0 (fordi man ikke kan dele kagen mellem nul personer).
Lad os tage et andet eksempel på omvendt proportionalitet. Vi skal køre 100 kilometer i bil. Jo hurtigere vi kører, des kortere tid tager turen (det er et tænkt eksempel, for i virkeligheden skal man naturligvis følge fartreglerne). Det skriver vi på denne måde:
x er hastigheden, og y er tiden.
Vi beregner, hvor mange timer turen vil tage at køre, hvis vi kører med en gennemsnitshastighed på henholdsvis 50, 80 og 100 kilometer i timen:
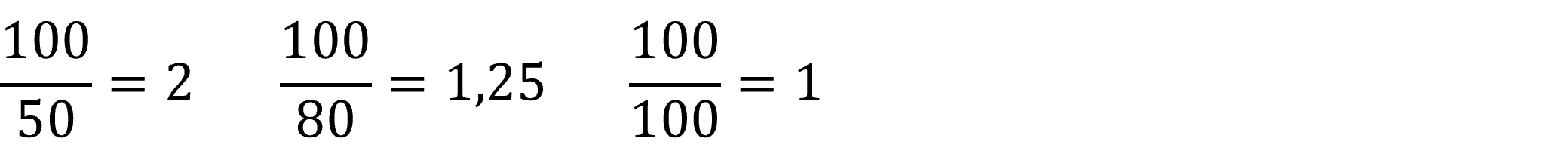
Skrevet med ord:
Hvis vi kører gennemsnitligt 50 km/t, tager turen 2 timer.
Hvis vi kører gennemsnitligt 80 km/t, tager turen 1 time og 15 minutter (vær opmærksom, når du omregner tid fra timer til minutter).
Hvis vi kører gennemsnitligt 100 km/t, tager turen 1 time.
Som du kan se, tager turen kortere tid, jo hurtigere vi kører – eller den tager længere tid, jo langsommere vi kører, om man vil. Forholdet mellem tid og hastighed er omvendt proportionalt, fordi øget fart medfører reduceret tid – og omvendt medfører reduceret fart øget tid.
Hvad kaldes graferne for omvendt proportionale funktioner?
Funktionsforskriften for omvendt proportionale funktioner kan vises med en graf ligesom alle andre funktioner. Denne graf kaldes en hyperbel og ser sådan her ud:
Grafen her viser funktionsforskriften for vores eksempel med sammenhængen mellem tid og hastighed på en 100 kilometers distance.
x-aksen viser hastigheden (km/t), og y-aksen viser tiden (antal timer). De tre punkter viser de tre beregninger, som vi lavede ovenfor, nemlig hvor lang tid det vil tage at køre 100 kilometer, hvis vi kører med en gennemsnitsfart på henholdsvis 50, 80 og 100 km/t.
Vi har tegnet grafen i programmet GeoGebra. Prøv at se, hvordan det ser ud, når vi indtaster fx denne funktion:
Hyperblen viser sig både i 1. og 3. kvadrant (læs om kvadranter i vores indlæg om funktioner og koordinatsystemet). For enhver hyperbel gælder det, at den aldrig vil ramme hverken x- eller y-aksen, hvor værdierne er 0 (x kan som nævnt ikke være 0, da man ikke kan dividere med 0, og man kan heller ikke dividere et tal med et andet tal og få 0, så derfor kan y heller ikke være 0).
I 1. kvadrant får man en positiv y-værdi, når man indsætter en positiv x-værdi, og i 3. kvadrant får man en negativ y-værdi, når man indsætter en positiv x-værdi. Hvis vi fx satte x-værdien -2 ind, ville y-værdien blive -0,5, fordi 1 divideret med -2 giver -0,5.
I vores eksempel giver det dog ikke mening, at “minus to” personer ville få “minus en halv” kage hver. I vores andet eksempel giver det heller ikke mening at tale om negativ tid og negativ hastighed. Man kan derfor specificere, at:
Altså at x ikke må være 0 (det gælder altid), og at x skal være større end 0, hvis man – som i vores eksempler – ikke kan tale om negative enheder.
Rent matematisk kan værdierne dog godt være negative – og det kan konstanten a også. Se her, hvordan grafen for denne funktionsforskriften ser ud, hvis a er -1:
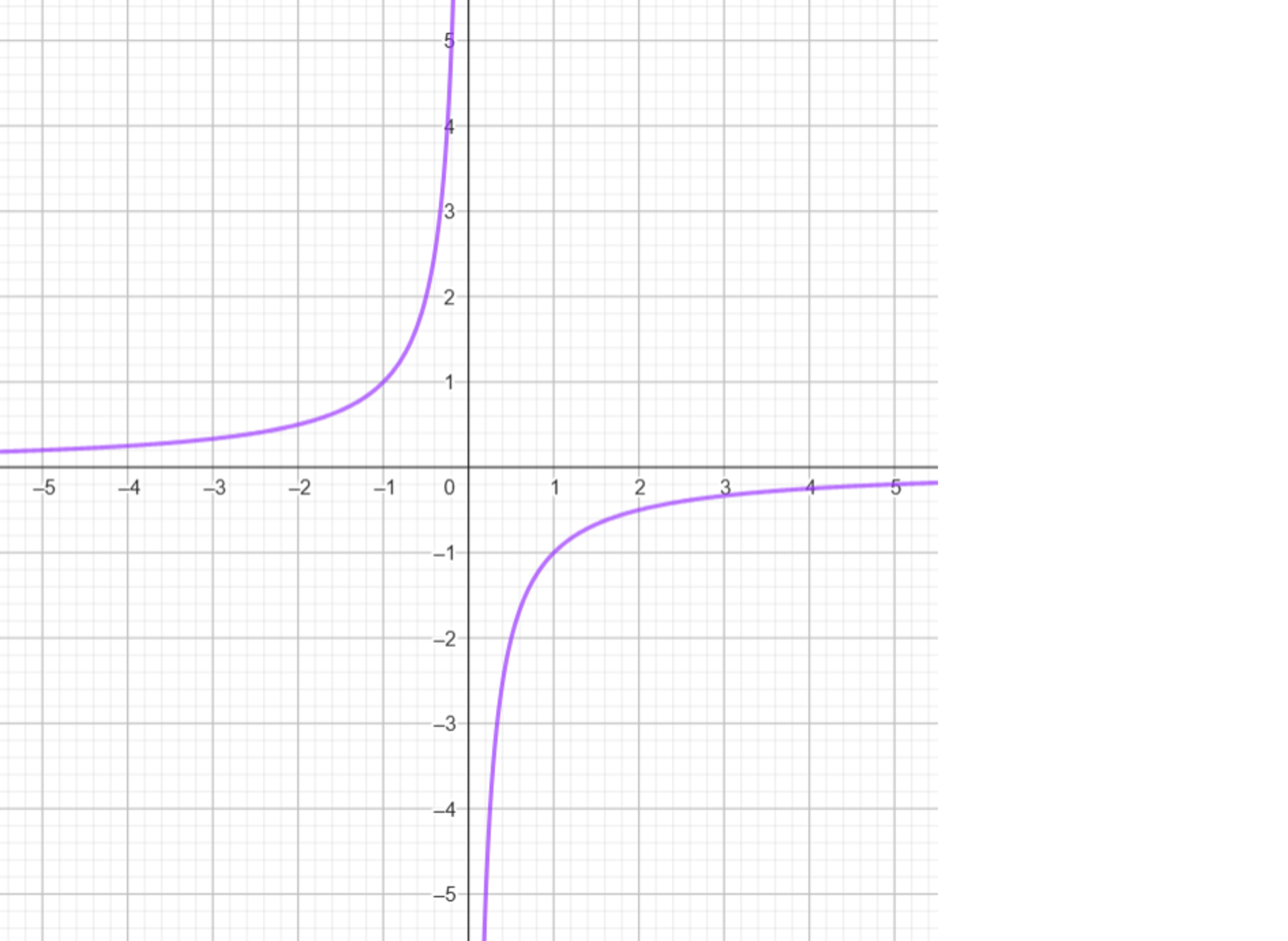
Her viser hyperblen sig i 2. og 4. kvadrant, så det gælder, at hvis x-værdien er negativ, er y-værdien positiv, og hvis x-værdien er positiv, er y-værdien negativ.
Dog giver det heller ikke her mening at koble funktionsforskrifterne og de tilhørende grafer til et tænkt eksempel, da enhederne (hvad end det er tid, distance, brøkdele af en kage eller noget fjerde) ikke er negative.