Funktioner minder om ligninger, men det er ikke helt det samme. I ligninger skal du finde frem til en bestemt værdi. I funktioner bestemmer du selv, hvad x-værdien skal være – til gengæld får vi en bestemt y-værdi.
I dette indlæg vil vi besvare følgende:
Hvad er funktioner?
x- og y-akse i et koordinatsystem
Hvilken graf hører til hvilken funktion?
Hvordan beregner man skæringspunktet mellem to funktioner?
Hvis søger hjælp til andre emner inden for matematik, kan du tjekke GoTutors matematikblog eller vores tilbud på lektiehjælp i matematik.
Hvad er funktioner?
Funktioner beskriver forholdet mellem to mængder. Hvert element i den ene mængde kan man knytte til et bestemt element i den anden mængde. Altså knytter man én bestemt x-værdi til én bestemt y-værdi.
Et eksempel kan være forholdet mellem prisen på benzin og antal liter benzin. Vi kan forestille os, at prisen på benzin er 12 kr. pr. liter. Hvis vi tanker 1 liter benzin på vores bil, skal vi betale 12 kroner. Hvis vi tanker 2 liter benzin, skal vi betale 24 kroner. Hvis vi tanker 20 liter benzin, skal vi betale 240 kroner. Altså er x-værdien (antal liter) knyttet til y-værdien (prisen), og man sætter en x-værdi ind for at finde en y-værdi.
Vi bestemmer selv, hvad x-værdien er – altså bestemmer vi selv, om vi vil tanke 10 liter, 22 liter, 31,5 liter eller noget helt andet. Prisen (y-værdien) afhænger af, hvor meget benzin vi tanker.
Mere generelt siger man, at x er en uafhængig variabel, som man selv kan bestemme. y-værdien er en afhængig variabel, fordi den afhænger af x-værdien. Man siger, at y er en funktion af x, så i stedet for at skrive y, skriver man som regel f(x) (man læser det som “f af x”). f er det navn, som man typisk giver en funktion, men det er også almindeligt at bruge g eller h – så skriver man bare g(x) eller h(x).
Vores eksempel med benzinens literpris på 12 kroner kan skrives som en funktion på denne måde:
f(x) = 12x
Vi kan sætte alle mulige tal ind på x’s plads i funktionen, som vi selv bestemmer:
f(1) = 12*1 = 12
f(2) = 12*2 = 24
f(10) = 12*10 = 120
f(22) = 12*22 = 264
f(31,5) = 12*31,5 = 378
Som du kan se, får man forskellige y-værdier, alt efter hvilken x-værdi man sætter ind i funktionen.
På samme måde er tangens, sinus og cosinus funktioner, fordi forholdet mellem to sider i en retvinklet trekant afhænger af størrelsen på en bestemt vinkel – men det kan du læse mere om i vores indlæg om trigonometri.
x- og y-akse i et koordinatsystem
Man kan også sætte sine x- og y-værdier ind i et koordinatsystem. Et koordinatsystem består af to akser, der står vinkelret på hinanden:
Den vandrette akse hedder x-aksen eller førsteaksen
Den lodrette akse hedder y-aksen eller andenaksen
Som vi gennemgik før, gælder det for funktioner, at y-værdien afhænger af x-værdien. I et koordinatsystem betyder det, at når vi vælger en værdi på x-aksen, får vi en værdi på y-aksen. Det kan fx være, at vores x-værdi er 1, og vores y-værdi er 2. Så skal vi gå 1 ud ad x-aksen, og 2 op ad y-aksen, så vi rammer dette punkt:
Man siger, at punktets x-koordinat er 1, og punktets y-koordinat er 2. Koordinatsættet skrives som (1, 2) – generelt (x, y).
Vi tager endnu et eksempel:
Her er koordinatet (2, -3), fordi x-værdien er 2, og y-værdien er -3. Som du kan se, ligger koordinatet i et andet område end det forrige eksempel, fordi y-værdien her er negativ. De to akser danner fire områder, som hedder kvadranter.
I 1. kvadrant er x-værdien positiv og y-værdien positiv
I 2. kvadrant er x-værdien negativ og y-værdien positiv
I 3. kvadrant er x-værdien negativ og y-værdien negativ
I 4. kvadrant er x-værdien positiv og y-værdien negativ
Et punkt kan også ligge lige på x-aksen, hvis x-værdien er 0, og/eller lige på y-aksen, hvis y-værdien er 0.
Som nævnt kan man også sætte funktioner ind i et koordinatsystem. Vi tager et eksempel med denne funktion:
f(x) = 2x + 1,5
Vi vælger x-værdierne -1, 0, 1 og 2 og sætter dem ind på x’s plads i funktionen:
f(-1) = 2*(-1) + 1,5 = -0,5
f(0) = 2*0 + 1,5 = 1,5
f(1) = 2*1 + 1,5 = 3,5
f(2) = 2*2 + 1,5 = 5,5
Det giver os fire y-værdier. Vi har nu fire koordinatsæt med én x-værdi og én y-værdi, som vi sætter ind i et koordinatsystem:
Hvis vi indsætter alle x-værdier, der findes, danner prikkerne en linje. Den linje er funktionens graf.
Grafen behøver ikke at være en lige linje. Grafer kan også se ud på disse måder:
Den lige graf og de tre andre grafer ovenfor tilhører fire forskellige slags funktioner:
Andengradspolynomium
En lineær funktion (den grønne graf) har forskriften:
f(x) = ax + b
En eksponentiel funktion (den brune graf) har forskriften:
f(x) = b ⋅ aˣ
En potensfunktion (den lilla graf) har forskriften:
f(x) = b ⋅ xª
Et andengradspolynomium (den blå graf) har forskriften:
f(x) = ax² + bx + c
Hvilken graf hører til hvilken funktion?
Det kan være, at du i en matematikopgave bliver bedt om at gøre rede for, hvilken graf der hører til hvilken funktion. Først vil vi vise, hvordan man kan vurdere, om en graf hører til en lineær funktion, en eksponentiel funktion, en potensfunktion eller et andengradspolynomium.
Ved lineære funktioner er grafen altid en helt lige linje. Hældningen kan være voksende eller aftagende, eller den kan være helt flad. Grafen går gennem to eller tre kvadranter i koordinatsystemet.
Ved eksponentielle funktioner er grafen formet som en bue. Hældningen kan enten være voksende eller aftagende. Grafen går altid kun gennem 1. og 2. kvadrant i koordinatsystemet.
Ved potensfunktioner er grafen som regel også formet som en bue, men den kan også være en lige linje. Det gælder dog, at potensfunktioners graf kun ligger inden for 1. kvadrant i koordinatsystemet.
Ved andengradspolynomier er grafen en parabel. Det betyder, at den enten ligner en glad mund eller en sur mund.
Nu har vi styr på, hvordan graferne til de forskellige funktionstyper ser ud. Men det kan også være, at du har en opgave, som går ud på at bestemme, hvilken forskrift der hører til hvilken graf. Fx kan vi få disse to billeder af to lineære grafer:
Vi får følgende to funktioner, som vi skal koble til den rigtige graf:
f(x) = -2x + 1
g(x) = 2x - 1
Vi kan starte med at se på, hvad a er i de to funktioner. For lineære funktioner gælder det, at hvis a er større end 0, er hældningen voksende, og hvis a er mindre end 0, er hældningen aftagende. I funktion f er a -2 (det vil sige mindre end 0), og derfor må den passe med grafen til højre, fordi grafen er nedadgående (aftagende). I funktion g er a 2 (det vil sige større end 0), og derfor må den passe med grafen til venstre, fordi grafen er opadgående (voksende).
Vi kunne også starte med at se på, hvad b er i de to funktioner. For lineære funktioner gælder det, at b angiver, hvor grafen skærer y-aksen. I funktion f er b 1, hvilket passer med grafen til højre. I funktion g er b -1, hvilket passer med grafen til venstre.
Ud fra graferne er det altså muligt at aflæse, hvad de tilhørende funktioner er.
Det er dog sværere at aflæse, hvis man har med eksponentielle funktioner at gøre, men her kan vi ud fra a se, om hældningen er voksende eller aftagende. Se billedet her:
Grafen til venstre har denne forskrift:
f(x) = 0,5 ⋅ 1,5ˣ
Her er a 1,5. Når a er større end 1 i eksponentielle funktioner, er hældningen voksende. Omvendt har grafen til højre denne forskrift:
f(x) = 0,5 ⋅ 0,5ˣ
Her er a 0,5. Når a er mellem 0 og 1 i eksponentielle funktioner, er hældningen aftagende.
Hvis vi skal vurdere forskellen på to grafer, som fx begge har en voksende hældning, kan vi kigge på, hvad b er i funktionen. For eksponentielle funktioner gælder det også, at b angiver, hvor grafen skærer y-aksen.
Grafen til venstre har denne forskrift:
f(x) = 3 ⋅ 2ˣ
Her er b lig med 3, og vi kan se, at grafen rigtigt nok skærer y-aksen ved y-værdien 3. Omvendt har grafen til højre denne forskrift:
f(x) = 1 ⋅ 2ˣ
Her er b 1, og det er også her, at grafen skærer y-aksen.
Så er der potensfunktioner, som kan se ud på fire forskellige måder, som i høj grad afgøres af værdien af a:
På billede 1 er a større end 1, så funktionen er stejlt voksende. Grafens forskrift er:
f(x) = 1 ⋅ x1,5
På billede 2 er a mellem 0 og 1, så funktionen her er også voksende, men den flader ud. Grafens forskrift er:
f(x) = 1 ⋅ x0,5
På billede 3 er a mindre end 0, så funktionen er aftagende. Grafens forskrift er:
f(x) = 1 ⋅ x-0,5
På billede 4 er a lig med 1, så funktionen er en lige linje med en hældning, der svarer til b. Grafens forskrift er:
f(x) = 1 ⋅ x1
Desuden gælder det for potensfunktioner, at b viser, hvad y-værdien er, når x-værdien er 1. Altså går grafen gennem punktet (1, b). Sådan kan vi se forskel på disse to grafer:
Grafen til venstre har denne forskrift:
f(x) = 1 ⋅ x1,5
Her er b 1, og vi kan se, at grafen rigtigt nok rammer koordinatet (1, 1). Omvendt har grafen til højre denne forskrift:
f(x) = 2 ⋅ x1,5
Her er b 2, så grafen rammer koordinatet (1, 2).
Til sidst vil vi se på forskellige grafer for andengradspolynomier. Andengradspolynomier har tre konstanter (a, b og c), som kan sige noget om, hvordan en funktions graf ser ud. Vi kigger først på a, som viser, om parablens grene vender opad eller nedad, og om parablen er smal eller bred. Sammenlign disse to billeder:
Grenene vender opad, fordi a er større end 0 i begge forskrifter.
På billedet til venstre er parablen smal, fordi a er numerisk stor. Grafen har denne forskrift:
f(x) = 3x² + x - 1
På billedet til højre er parablen bred, fordi a er numerisk lille. Grafen har denne forskrift:
f(x) = 0,3x² + x - 1
Lad os nu sammenligne disse:
Grenene vender nedad, fordi a er mindre end 0 i begge forskrifter.
På billedet til venstre er parablen smal, igen fordi a er numerisk stor. Grafen har denne forskrift:
f(x) = -3x² + x - 1
På billedet til højre er parablen bred, igen fordi a er numerisk lille. Grafen har denne forskrift:
f(x) = -0,3x² + x - 1
For andengradspolynomier gælder det, at b angiver, hældningen for tangenten til grafen. Tangenten er en lige linje, som kun rammer grafen der, hvor grafen skærer y-aksen. Sammenlign disse tre billeder:
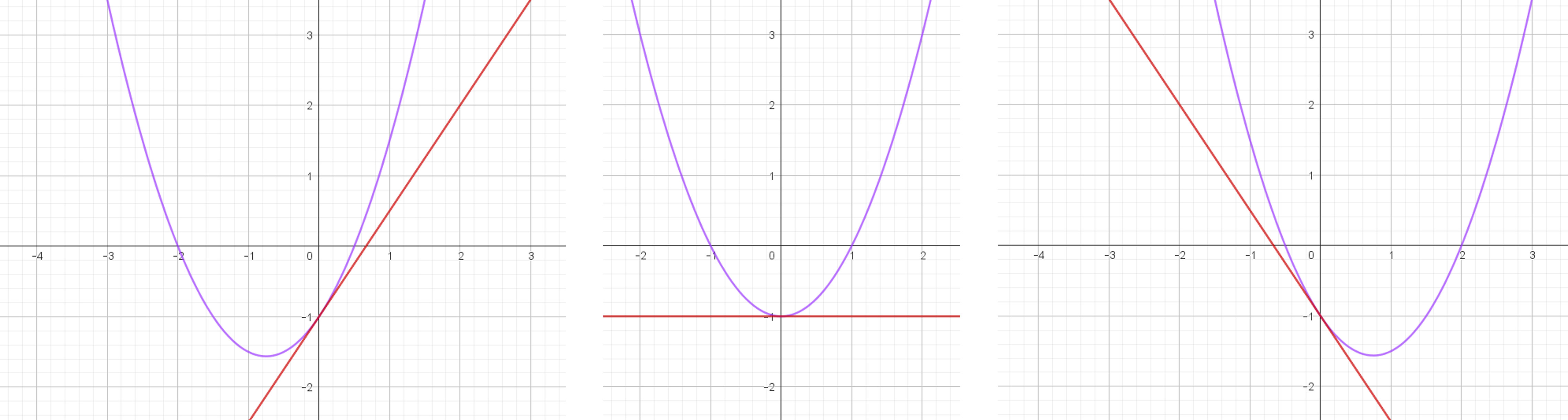
Det er ikke sikkert, at tangenten er vist i den opgave, som du sidder med, men vi kan alligevel se forskel.
Grafen til venstre har denne forskrift:
f(x) = x² + 1,5x - 1
Her er b 1,5, og når b er større end 1, ligger parablens toppunkt til venstre for y-aksen.
Grafen i midten har denne forskrift:
f(x) = x² - 1
Her er b 0, og når b er lig med 0, skærer parablens toppunkt y-aksen.
Grafen til højre har denne forskrift:
f(x) = x² - 1,5x - 1
Her er b -1,5, og når b er mindre end 1, ligger parablens toppunkt til højre for y-aksen.
Til sidst kan vi også vurdere forskel ud fra c-værdien. c angiver, hvor grafen skærer y-aksen – som vi har set, handler det bare om at aflæse billederne.
Hvordan beregner man skæringspunktet mellem to funktioner?
Hvis man har to funktioner, kan man beregne skæringspunktet – det vil sige det eller de steder, hvor graferne skærer hinanden. På dette billede skærer graferne for to lineære funktioner hinanden:
Vi får at vide, hvad funktionerne for de to grafer er:
f(x) = 3x - 2
g(x) = -2x + 8
For at beregne skæringspunktet skal vi sætte de to forskrifter lig hinanden:
3x - 2 = -2x + 8
Vi har nu en ligning. Hvis du ikke har styr på reglerne for, hvordan man løser en ligning, kan du læse vores indlæg om ligninger.
Vi samler x’erne på den ene side af lighedstegnet, og vi samler tallene på den anden side:
3x + 2x = 8 + 2
5x = 10
x = 2
Nu ved vi, at skæringspunktets x-værdi er 2. Det sætter vi ind på x’s plads i en af funktionerne, så vi får en y-værdi:
f(2) = 3*2 - 2 = 4
Sådan har vi beregnet, at skæringspunktet har koordinatet (2, 4). Det kan vi også aflæse på billedet, men det er godt at kende regnereglerne, hvis man får en opgave, hvor der ikke følger et billede med, eller hvis opgaven beder dig om at beregne skæringspunktet – ikke aflæse.
Vi tager endnu et eksempel, hvor vi har en lineær funktion og et andengradspolynomium. Her har vi to skæringspunkter:
Vi får at vide, at funktionerne er:
f(x) = 2x² - 2x + 1
g(x) = 2x + 1
Igen skal vi sætte de to forskrifter lig hinanden:
2x² - 2x + 1 = 2x + 1
Vi skal ændre ligningen, så der står 0 på den ene side af lighedstegnet:
2x² - 2x + 1 - 2x - 1 = 0
Vi har nu en andengradsligning, fordi et af leddene er opløftet i anden potens. Hvis du ikke har styr på reglerne for, hvordan man løser andengradsligninger, kan du læse vores indlæg om andengradsligninger - hvor du i øvrigt også kan læse lidt mere om andengradspolynomier.
Vi starter med at reducere:
2x² - 4x = 0
Vi har altså nu andengradsligning, hvor a = 2, b = -4 og c = 0. Dernæst skal vi finde diskriminanten, som har formlen d = b² - 4ac.
d = (-4)² - 4*2*0 = 16 - 0 = 16
Diskriminanten er positiv, så vi har to løsninger:
Nu har vi vores to x-værdier for skæringspunkterne: 0 og 2. Som altid finder vi y-værdierne ved at sætte x-værdierne ind i forskrifterne. Det er lige meget, om vi vælger forskrift f eller g, men her er det nemmest at tage forskrift g.
g(0) = 2*0 + 1 = 1
g(2) = 2*2 + 1 = 5
Sådan har vi beregnet koordinaterne for skæringspunkterne til at være (0, 1) og (2, 5).