En cirkel er en rund figur, som har et areal og en omkreds. En cirkels areal svarer til, hvor stor dens flade er, og en cirkels omkreds svarer til, hvor langt der er rundt om cirklen. I dette indlæg viser vi en række formler, som du kan bruge til at finde arealet, omkredsen, radiussen eller diameteren af en cirkel, når du kender mindst ét af de andre mål.
Derefter kommer vi ind på andre mål i en cirkel: korder, cirkelbuer, cirkelafsnit, cirkeludsnit og pilhøjder. Vi slutter af med at vise formlerne for areal og omkreds af en anden rund figur, nemlig en ellipse.
Altså kommer vi ind på:
Hvordan finder man arealet af en cirkel?
Hvordan finder man omkredsen af en cirkel?
Hvordan finder man radius af en cirkel, når man kender arealet?
Hvordan finder man diameteren af en cirkel, når man kender arealet?
Hvordan finder man radius af en cirkel, når man kender omkredsen?
Hvordan finder man diameteren af en cirkel, når man kender omkredsen?
Hvordan finder man arealet af en cirkel, når man kender omkredsen?
Hvordan finder man omkredsen af en cirkel, når man kender arealet?
Hvad er korder?
Hvad er en cirkelbue?
Hvad er radianer?
Hvad er et cirkelafsnit?
Hvad er et cirkeludsnit?
Hvad er pilhøjden?
Hvordan finder man arealet af en ellipse?
Hvordan finder man omkredsen af en ellipse?
Hvordan finder man arealet af en cirkel?
For at finde arealet af en cirkel skal man opløfte cirklens radius i anden potens og gange med pi (≈ 3,14). Formlen for arealet af en cirkel ser sådan ud:

A står for ‘areal’, r står for ‘radius’, og 𝝅 er tallet pi, som er 3,14159… (med uendeligt mange decimaler).
En cirkels radius er afstanden fra cirklens centrum ud til cirklens periferi. På billedet nedenunder er radiussen vist med den stiplede linje, som går fra centrum (ved den grønne prik) til periferien (som ved den gule prik). Periferien er ethvert punkt på den blå linje, som alle har samme afstand til centrum.

Lad os kigge på et eksempel. Vi vil beregne arealet af en cirkel, der har en radius på 4 cm.

Vi sætter derfor 4 ind på r’s plads i formlen og får dette resultat:

Vi afrunder typisk med to decimaler, så vores svar er, at cirklens areal er omkring 50,27 cm² (50,27 kvadratcentimeter).
Hvordan finder man omkredsen af en cirkel?
For at finde omkredsen af en cirkel skal man gange cirklens diameter med pi. Formlen for omkredsen af en cirkel ser sådan ud:

O står for ‘omkreds’, d står for ‘diameter’, og 𝝅 er som nævnt tallet pi (≈ 3,14).
En cirkels diameter er afstanden fra periferi til periferi igennem centrum. Det vil sige, at en cirkels diameter er dobbelt så lang som radiussen, og ligeledes er radiussen halvt så lang som diameteren.

Vi kigger på et eksempel. Vi har den samme cirkel fra før, hvor diameteren er 8 cm, og nu vil vi gerne beregne omkredsen af cirklen.

Sådan har vi beregnet, at cirklens omkreds er cirka 25,13 cm.
Fordi diameteren er det samme som to gange radius, kan formlen også se sådan her ud:

Husk at skrive den rigtige enhed, når du skriver dit resultat. Når man finder en omkreds, finder man en længde, og man skriver derfor længden i centimeter, meter, millimeter eller lignede (forkortet cm, m, mm). Når man derimod finder et areal, finder man en overflade, og man skriver derfor overfladen i kvadratcentimer, kvadratmeter, kvadratmillimeter eller lignende (forkortet cm2, m2, mm2).
Hvordan finder man radius af en cirkel, når man kender arealet?
Vi har set, hvordan man finder en cirkels areal, når man kender cirklens radius. Man bruger denne formel:

Men hvad gør man, hvis man omvendt kender arealet og gerne vil finde radiussen? For at finde radiussen skal vi isolere r i formlen. Det vil sige, at r skal stå alene på den ene side af lighedstegnet, mens de andre tal og variabler står på den anden side af lighedstegnet.
Først flytter vi pi over på den anden side. I formlen skal man gange med pi, så vi bruger den modsatte funktion, nemlig at dividere med pi – på begge sider af lighedstegnet:

For at lave r² om til r skal vi bruge den modsatte funktion af at opløfte i anden, nemlig at tage kvadratroden på begge sider af lighedstegnet:

Når man kender arealet af en cirkel og skal finde dens radius, skal man derfor bruge denne formel:

Lad os beregne et eksempel, hvor vi har en cirkel med et areal på 20 cm².

Sådan har vi beregnet, at en cirkel med et areal på 20 cm² har en radius på cirka 2,52 cm.
Hvordan finder man diameteren af en cirkel, når man kender arealet?
Når vi kender arealet af en cirkel, kan vi også finde diameteren på næsten samme måde som før, fordi diameteren som nævnt er dobbelt så lang som radiussen. Formlen ser sådan ud:

Cirklen med et areal på 20 cm² har dermed en diameter på cirka 5,05 cm (dobbelt så lang som radiussen).
Hvordan finder man radius af en cirkel, når man kender omkredsen?
Vi har set, at formlen til at finde omkredsen af en cirkel, når man kender dens radius, ser sådan her ud:

Hvis vi omvendt skal finde en cirkels radius, når vi kender omkredsen, skal vi isolere r i ligningen. I formlen ganger vi med pi, så vi starter med at dividere med pi på begge sider af lighedstegnet:

For at lave 2r om til r skal vi dividere med 2 på begge sider af lighedstegnet:

Når man kender omkredsen af en cirkel og skal finde dens radius, skal man derfor bruge denne formel:

Vi ser på et eksempel, hvor vi har en cirkel med en omkreds på 35 cm. Vi sætter derfor 35 ind på O’s plads i formlen:

Sådan har vi beregnet, at en cirkel med en omkreds på 35 cm har en radius på cirka 5,57 cm.
Hvordan finder man diameteren af en cirkel, når man kender omkredsen?
Igen er formlen næsten den samme som før, fordi diameteren er dobbelt så lang som radiussen.

Cirklen med en omkreds på 35 cm har dermed en diameter på cirka 11,14 cm (dobbelt så lang som radiussen).
Hvordan finder man arealet af en cirkel, når man kender omkredsen?
Vi har to ligninger, hvor vi har isoleret r. Man kan bruge den ene til at finde arealet af en cirkel, nemlig denne:

Man kan bruge den anden til at finde omkredsen af en cirkel, nemlig denne:

Når kvadratroden af A divideret med 𝝅 og O divideret med 2𝝅 begge har samme værdi som r, har de også samme værdi som hinanden:

Når vi kender omkredsen af en cirkel og vil finde arealet, skal vi have isoleret A i formlen. Først fjerner vi kvadratroden ved at opløfte i anden potens på begge sider af lighedstegnet:

På venstre side af lighedstegnet er A divideret med pi, så hvis der kun skal stå A, skal vi gange med pi på begge sider:

Nu har vi isoleret A og dermed fundet formlen.
Lad os derfor se på et eksempel. Vi har en cirkel med en omkreds på 18 cm, og vi er interesserede i at beregne arealet. Vi sætter 18 ind på O’s plads i ligningen.

Sådan har vi beregnet, at en cirkel med en omkreds på 18 cm har et areal på cirka 25,78 cm².
Hvordan finder man omkredsen af en cirkel, når man kender arealet?
Ovenover har vi fundet sammenhængen mellem omkreds og areal i en cirkel med denne formel:

Før isolerede vi A, men nu er vi interesserede i at finde omkredsen, så nu isolerer vi O i ligningen. Det kan vi gøre ved at gange med 2𝝅 på begge sider af lighedstegnet:

Nu har vi isoleret O og dermed fundet formlen.

Lad os se på et eksempel. Vi har en cirkel med et areal på 50 cm², og vi vil beregne omkredsen. Regnestykket ser sådan ud:

Cirklens omkreds er cirka 25,07 cm.
Hvad er korder?
En korde i en cirkel er en linje, der går mellem to punkter på cirklens periferi, som vist her:

Mellem hvert af de to punkter kan der dannes to radier (radius i flertal) ind til cirklens centrum. Disse danner en vinkel (v), som vi skal kende for at beregne længden af korden.

Formlen for at beregne kordens længde er:

K er kordens længde, r er radius, sin er den trigonomiske funktion sinus, og v er vinklen målt i grader.
Lad os beregne et eksempel, hvor vi vil finde længden af en korde mellem to punkter. Vi har en cirkel med en radius på 3 cm, og vinklen mellem de to radier (der går ud til de to punkter) er 150 grader:

Vores korde har en længde på cirka 5,8 cm.
Hvad er en cirkelbue?
Det stykke af cirklens periferi, der går mellem to punkter på periferien, kaldes en cirkelbue. På det forrige billede (hvor vi tegnede en korde mellem to de punkter) kan vi i stedet tegne en cirkelbue mellem de to punkter:

Det gule stykke er et eksempel på en cirkelbue.
Man kan finde buelængden på to måder: enten ved at kende vinklen i grader eller ved at kende vinklens radiantal (vi gennemgår radianer i næste afsnit). Hvis v er angivet i grader, skal man bruge denne formel:

L er cirkelbuens længde, v er vinklen mellem de to radier, og r er radius.
Hvis v er angivet i radianer, skal man bruge denne formel:

Lad os beregne et eksempel med de samme mål som før. Vores radius er 3 cm, og vores vinkel er 150 grader:

Cirkelbuen har dermed en længde på 7,85 cm.
Hvad er radianer?
En radian er en måleenhed, der baserer sig på cirklens radius. 1 radian svarer til en vinkelstørrelse på cirka 57,3 grader:

Hvis vi lægger radianerne sammen, indtil vi rammer en vinkel på 180 grader, får vi…

… 3,14 radier – et tal, der svarer til pi. Som vi har set, er omkredsen to gange pi. En halv omkreds er pi, og vinklen i en halv cirkel er 180 grader. 180 divideret med pi er 57,2958…, og derfor har en radian en vinkel på denne størrelse.
Hvis man har en vinkel mellem to radier i en cirkel, kan man måle vinklen i radianer i stedet for grader. Man skal enten kende vinklen i grader eller længden af cirkelbuen:


Hvad er et cirkelafsnit?
Et cirkelafsnit er det område mellem en korde og cirklens periferi, som vist med det lyserøde område her:

Bemærk, at der er forskel på et cirkelafsnit og et cirkeludsnit.
Man kan finde arealet af et cirkeludsnit med denne formel:

Her er v angivet i grader.
Vi beregner et eksempel. Vi har en cirkel med en radius på 10 cm, og vinklen mellem to radier er 90 grader:
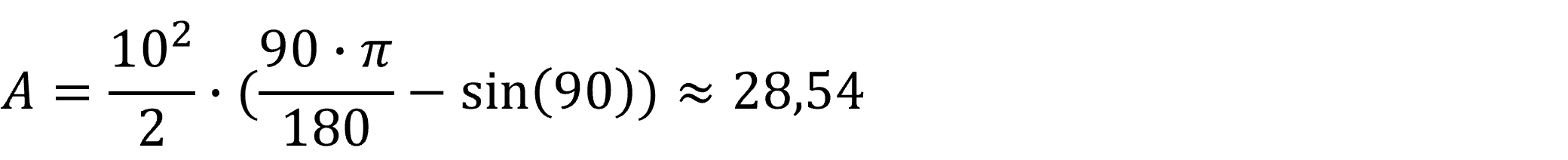
Vores cirkelafsnit har dermed et areal på 28,54 cm2.
Hvad er et cirkeludsnit?
Et cirkeludsnit er det område mellem to radier og cirklens periferi, som vist med det lyserøde område her:

Et cirkeludsnit kaldes også en sektor.
Hvis vinklen (v) er angivet i radianer, finder man arealet af et cirkeludsnit med denne formel:

Hvis vinklen (v) i stedet er angivet i grader, finder man arealet af et cirkeludsnit med denne formel:

Vi beregner et eksempel, hvor cirklens radius er 8 cm, og vinklen mellem to radier er 60 grader:

Sådan har vi beregnet, at vores cirkeludsnit har et areal på 33,51 cm2.
Hvad er pilhøjden?
Pilhøjden i en cirkel er længste linje, som går vinkelret på korden fra periferien, som vist her:

Man finder længden af pilhøjden med denne formel:

h er pilhøjden, r er radius, cos er den trigonomiske funktion cosinus, og v er vinklen mellem de to radier målt i grader.
Lad os beregne et eksempel, hvor vi har en cirkel med en radius på 11 cm og en vinkel på 120 grader:
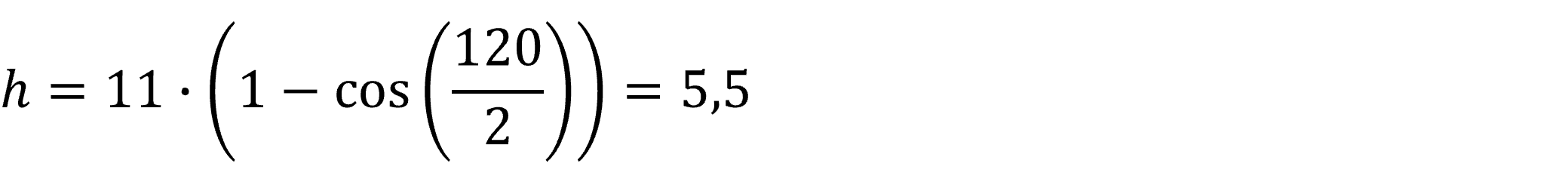
Vores pilhøjde er dermed 5,5 cm lang.
Hvordan finder man arealet af en ellipse?
En ellipse er en cirkel, der er presset sammen, så afstanden fra centrum til periferi ikke er den samme i alle punkter. På billedet nedenunder kan du se en ellipse, hvor a er den korteste radius, og b er den længste radius.

Man finder arealet af en ellipse ved at gange den korteste radius med den længste radius med pi:

Lad os beregne et eksempel, hvor a er 3 cm, og b er 4 cm:

Vores ellipse har dermed et areal på 37,7 cm2.
Hvordan finder man omkredsen af en ellipse?
Faktisk findes der ikke en formel, der præcist kan beregne omkredsen af en hvilken som helst ellipse. Man kan beregne omkredsen af en cirkel, fordi der er en klar sammenhæng mellem en cirkels radius og konstanten pi. Ellipser har derimod forskellige størrelsesforhold.
Der findes dog en formel, der kommer tæt på:

Med denne formel beregner vi et eksempel, hvor a er 3 cm, og b er 4 cm:

Ellipsen har en omkreds på cirka 22,21 cm.
Areal og omkreds af cirkel
En cirkel er en todimensionel figur. Det betyder, at man kan beregne arealet af en cirkel (hvor stor dens flade er), og man kan beregne omkredsen af en cirkel (hvor langt der er rundt om cirklen). Man kan ikke tale om at finde rumfanget af en cirkel eller overfladearealet af en cirkel, for det gælder kun ved tredimensionelle figurer.
Se på figurerne nedenunder. De gule figurer (en cirkel og et rektangel) har to dimensioner, og de grønne figurer (en cylinder og en kasse) har tre dimensioner. Todimensionelle figurer er flade, mens tredimensionelle figurer har dybde.
